
 如图,将矩形纸片ABCD沿AE折叠,点B恰好落在AC上的点F处,若AB=1,BC=2,求BE的长.
如图,将矩形纸片ABCD沿AE折叠,点B恰好落在AC上的点F处,若AB=1,BC=2,求BE的长. 分析 在Rt△ABC中由勾股定理可求得AC=$\sqrt{5}$,设BE=x,则EC=2-x.由翻折的性质可知BE=EF=x,AF=AB=1,于是可求得FC=$\sqrt{5}$-1,最后在Rt△EFC中,由勾股定理列方程求解即可.
解答 解;在Rt△ABC中由勾股定理得:AC=$\sqrt{A{B}^{2}+C{B}^{2}}$=$\sqrt{5}$.
设BE=x,则EC=2-x.由翻折的性质可知:∠B=∠EFA=90°,BE=EF=x,AF=AB=1.
FC=AC-AF=$\sqrt{5}$-1.
在Rt△EFC中,由勾股定理得:EC2=EF2+FC2,即${x}^{2}+(\sqrt{5}-1)^{2}=(2-x)^{2}$.
解得:x=$\frac{\sqrt{5}-1}{2}$,即BE=$\frac{\sqrt{5}-1}{2}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用,依据勾股定理列出关于x的方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
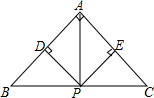 在△ABC,点P是BC边的中点,PD⊥AB于点D,PE⊥AC于点E,求证:
在△ABC,点P是BC边的中点,PD⊥AB于点D,PE⊥AC于点E,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
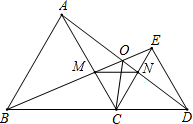 如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连OC、MN,则下列结论①AD=BE;②AN=BM;③MN∥BD;④∠BOC=∠DOC;⑤若∠ADE=20°,则∠BED=100°;⑥OB=AO+OC,其中正确的结论个数有( )
如图,已知△ABC和△CDE均是等边三角形,点B、C、D在同一条直线上,BE与AD交于点O,AD与CE交于点N,AC与BE交于点M,连OC、MN,则下列结论①AD=BE;②AN=BM;③MN∥BD;④∠BOC=∠DOC;⑤若∠ADE=20°,则∠BED=100°;⑥OB=AO+OC,其中正确的结论个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.
已知.如图,在正方形(四边相等,四个内角都为90°)ABCD中,过顶点D作射线交AB于E,过点B作BF⊥DE,F为垂足,联结AF,过点A作AG⊥AF交DE于G.求证:∠AGD=135°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,D是斜边AB的中点.点P从点B出发沿BC方向匀速运动,速度为1cm/s;同时,点Q从点A出发,沿AC方向匀速运动,速度为2cm/s.当点Q停止运动时,点P也停止运动.连接PQ、PD、QD.设运动时间为t(s)(0<t<4).
已知:如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,D是斜边AB的中点.点P从点B出发沿BC方向匀速运动,速度为1cm/s;同时,点Q从点A出发,沿AC方向匀速运动,速度为2cm/s.当点Q停止运动时,点P也停止运动.连接PQ、PD、QD.设运动时间为t(s)(0<t<4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.
如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com