
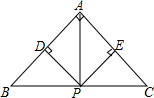
 在△ABC,点P是BC边的中点,PD⊥AB于点D,PE⊥AC于点E,求证:
在△ABC,点P是BC边的中点,PD⊥AB于点D,PE⊥AC于点E,求证:分析 (1)由HL证明Rt△BPD≌Rt△CPE,得出对应角相等∠B=∠C,由等角对等边即可得出AB=AC即可;
(2)由等腰三角形的三线合一性质得出∠BAP=∠CAP,再由角平分线的性质定理即可得出结论.
解答 证明:(1)∵点P是BC边的中点,
∴BP=CP,
∵PD⊥AB于点D,PE⊥AC于点E,
∴∠PDB=∠PEC=90°,
在Rt△BPD和Rt△CPE中,$\left\{\begin{array}{l}{BP=CP}\\{PD=PE}\end{array}\right.$,
∴Rt△BPD≌Rt△CPE(HL),
∴∠B=∠C,
∴AB=AC;
(2)∵AB=AC,点P是BC边的中点,
∴∠BAP=∠CAP,
∵PD⊥AB于点D,PE⊥AC于点E,
∴PD=PE.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、角平分线的性质定理;熟练掌握全等三角形的判定方法和等腰三角形的判定与性质是解决问题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:选择题
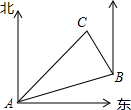 同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )
同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )| A. | 700米 | B. | 700$\sqrt{3}$米 | C. | 800米 | D. | 800$\sqrt{3}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
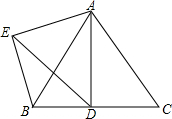 如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
如图,△ABC为等边三角形,点D为BC边上一动点(不与B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com