先化简:$÷\frac{{a}^{2}-4a+4}{{a}^{2}-1}$.再选则一个你最喜欢的a的值代入求值．题目和参考答案——青夏教育精英家教网—

10．先化简：（1-$\frac{3}{a+1}$）$÷\frac{{a}^{2}-4a+4}{{a}^{2}-1}$，再选则一个你最喜欢的a的值代入求值．

分析首先计算括号内的分式，把除法转化为乘法，分子的分母分解因式，然后进行约分即可化简，然后代入适当的值，求解．其中a不能代入1、-1和2．

解答解：原式=$\frac{a+1-3}{a+1}$•$\frac{（a+1）（a-1）}{（a-2）^{2}}$
=$\frac{a-2}{a+1}$•$\frac{（a+1）（a-1）}{（a-2）^{2}}$
=$\frac{a-1}{a-2}$．
当a=0时，原式=$\frac{1}{2}$．

点评本题考查了分式的化简求值，取喜爱的数代入求值时，要特注意原式及化简过程中的每一步都有意义，注意a不能取到的值．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

20．可以把代数式2ax²-12ax+18a分解因式为：2a（x-3）²．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．

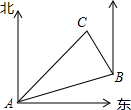同学甲要从A点出发到距离A点1000米的C地去，他先沿北偏东70°方向到达B地，然后再沿北偏西20°方向走了600米到达目的地C，由此可知AB之间的距离为（　　）

A．

700米

B．

700$\sqrt{3}$米

C．

800米

D．

800$\sqrt{3}$米

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．

如图，利用一面足够长的墙，用铁栅栏围成一个矩形自行车场地ABCD，在AB和BC边各有一个2米宽的小门（不用铁栅栏），设矩形ABCD的宽AD为x米，矩形的长为AB（且AB＞AD）．
（1）若所用铁栅栏的长为40米，用含x的代数式表示矩形的长AB；
（2）在（1）的条件下，若使矩形场地面积为192平方米，则AD、AB的长应分别为多少米？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．

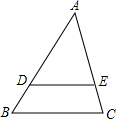如图，在△ABC中，点D、E分别在边AB、AC上，$\frac{AD}{AB}$=$\frac{3}{4}$，AE=3，CE=1，BC=6．
（1）求DE的长；
（2）过点D作DF∥AC交BC于F，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，求向量$\overrightarrow{DF}$（用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示）

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

15．

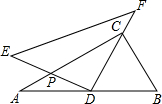将一副三角尺如图摆放，其中在Rt△ABC中，∠ACB=90°，∠B=60°，在Rt△EDF中，∠EDF=90°，∠E=45°．点D为边AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转角α（0°＜α＜60°）后得△E′DF′，DE′交AC于点M，DF′交BC于点N，那么$\frac{PM}{CN}$的值为$\frac{\sqrt{3}}{3}$．