
分析 (1)利用旋转的性质和平行线的性质进行计算即可;
(2)利用(1)中的结论解答即可;
(3)利用(1)中的结论得出关系式,进而解出取值范围即可;
应用提升:
(1)①连接AC'和AC,利用旋转的性质和平行线的性质进行计算即可;
②利用①中的结论得出关系式,进而得出代数式即可.
解答 解:(1)如图1:
∵AB∥CC',
∴∠1=∠BAC=40°,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=180°-40°-40°=100°;
(2)如图2:
∵AB∥CC',
∴∠1=∠BAC=70°,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=180°-70°-70°=40°;
故答案为:40°;
(3)∵AB∥CC',
∴∠1=∠BAC=α,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=β=180°-α-α=180°-2α,
∴α的取值范围0°<α<90°;
故答案为:180°-2α,0°<α<90°;
应用提升:
(1)①连接AC'和AC,如图3: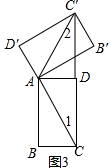
∵矩形ABCD,BC=1,AB=$\sqrt{3}$,
∴∠BAC=30°,
∵AB∥CC',
∴∠1=∠BAC=30°,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=180°-30°-30°=120°;
故答案为:120°;
②∵AB∥CC',
∴∠1=∠BAC=α,
由旋转可得:AC=AC',
∴∠1=∠2,
∴∠CAC'=β=180°-α-α=180°-2α,
所以α=90°-$\frac{1}{2}β$.
故答案为:90°-$\frac{1}{2}β$.
点评 此题考查几何变换问题,关键是根据旋转的性质和平行线的性质进行分析解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的角是对顶角 | B. | 两点之间线段最短 | ||
| C. | 两直线平行,同旁内角相等 | D. | 若$\sqrt{{a}^{2}}$=a,则a>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com