
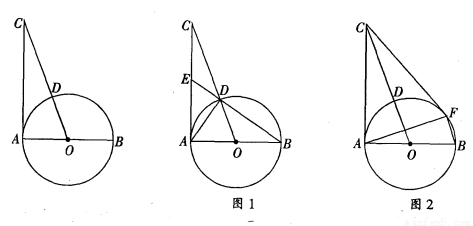
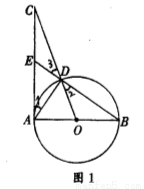
(本题满分12分)如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D.
(1)如图1,连接BD并延长BD交AC于点E,连接AD.
①证明:△CDE∽△CAD;
②若AB=2,AC=2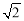 .求CD和CE的长;
.求CD和CE的长;
(2)如图2,过点C作⊙O的另一条切线,切点为F,连结AF、BF,若OC=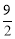 BF,求
BF,求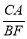 的值.
的值.
(1)①见解析;②CD=2;CE=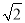
(2)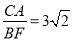
【解析】
试题分析:(1)①因为两个三角形有一公共角,所以只需要再证明一个角对应相等即可,根据条件AC是⊙O的切线,AB是⊙O的直径,利用互余的关系可证∠CAD=∠CDE;②在Rt△AOC中,由勾股定理可求OC=3,由△CDE∽△CAD,可得出CE=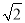 ;(2)设圆的半径为r,由△ABF∽△COA,得
;(2)设圆的半径为r,由△ABF∽△COA,得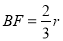 ,在Rt△COA中,由勾股定理可得CA=
,在Rt△COA中,由勾股定理可得CA=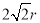 ,从而可得
,从而可得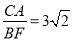 .
.
试题解析:(1)①证明:因为AC是⊙O的切线,所以∠1+∠BAD=90°,又因为AB是⊙O的直径,所以∠B+∠BAD=90°,所以∠1=∠B, 又OB=OD,所以∠2=∠B,又∠2=∠3,所以∠3=∠B,所以∠1=∠3,又∠C=∠C,所以△CDE∽△CAD;
②在Rt△AOC中,OC=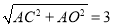 ,所以CD=OC-OD=3-1=2,又△CDE∽△CAD,所以
,所以CD=OC-OD=3-1=2,又△CDE∽△CAD,所以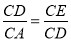 ,所以
,所以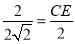 ,CE=
,CE= 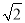 ;(2)设圆的半径为r,由△ABF∽△COA,,所以
;(2)设圆的半径为r,由△ABF∽△COA,,所以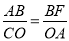 ,所以
,所以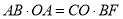 ,又OC=
,又OC=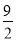 BF,AB=2r,OA=r,所以
BF,AB=2r,OA=r,所以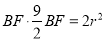 ,所以
,所以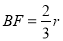 ,OC=3r,在Rt△COA中,由勾股定理可得CA=
,OC=3r,在Rt△COA中,由勾股定理可得CA=
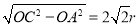 ,所以
,所以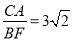 .
.
考点:1.切线的性质;2. 勾股定理;3.相似三角形的判定与性质.


科目:初中数学 来源:2014-2015学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:填空题
观察下列等式:
12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
……
在上面的等式中,等式两边的数字分别是对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据以上各等式反映的规律,使下面等式成为“数字对称等式”:
52× = ×25;
(2)设这类等式左边的两位数中,个位数字为a,十位数字为b,且2≤a+b≤9,则用含a,b的式子表示这类“数字对称等式”的规律是
.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区八年级上学期期末考试数学试卷(解析版) 题型:选择题
一个多边形的内角和是外角和的2倍,则这个多边形是
A. 四边形 B. 五边形 C. 六边形 D. 八边形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省诸城市九年级下学期开学检测数学试卷(解析版) 题型:选择题
将100个数据分成①~⑧组,如下表所示:
组号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ |
频数 | 4 | 8 | 12 |
| 24 | 18 | 7 | 3 |
那么第④组的频率为( ).
A.24 B.26 C.0.24 D.0.26
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分6分)
(1)已知x+y=8,x2-y2=32,则x- y= ;
(2)已知x>y>0,x+y=8,x2+y2=40,求x-y的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:填空题
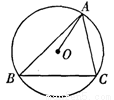
如图,△ABC内接于⊙O,AO=2,BC=2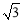 ,则∠BAC的度数为 °.
,则∠BAC的度数为 °.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:解答题
为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,二中学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间,根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:

(1)本次调查的学生人数是 人.
(2)图2中α是 度,并将图1条形统计图补充完整.
(3)请估算该校九年级学生自主学习的时间不少于1.5小时有 人.
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市毕业班正月联考数学试卷(解析版) 题型:选择题
已知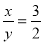 ,那么下列等式中,不一定正确的是( )
,那么下列等式中,不一定正确的是( )
A.x+y=5 B.2x=3y C.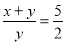 D.
D.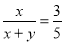
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com