
【题目】如图,已知抛物线的顶点坐标为![]() ,且经过点
,且经过点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() .
.
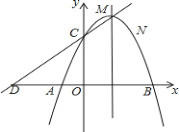
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若直线
若直线![]() 经过
经过![]() 、
、![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,试证明四边形
,试证明四边形![]() 是平行四边形;
是平行四边形;
![]() 点
点![]() 在抛物线的对称轴
在抛物线的对称轴![]() 上运动,请探索:在
上运动,请探索:在![]() 轴上方是否存在这样的
轴上方是否存在这样的![]() 点,使以
点,使以![]() 为圆心的圆经过
为圆心的圆经过![]() 、
、![]() 两点,并且与直线
两点,并且与直线![]() 相切?若存在,请求出点
相切?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)A(-1,0)B(3,0)C(0,3)
(2)平行四边形
(3)(1,![]() )
)
【解析】
试题(1)根据顶点式设抛物线解析式为y=a(x-1)2+4,将N(2,3)代入求a,确定抛物线解析式,根据抛物线解析式求点A、B、C的坐标;
(2)根据M、C两点坐标求直线y=kx+t解析式,得出D点坐标,求线段AD,由C、N两点坐标可知CN∥x轴,再求CN,证明CN与AD平行且相等,判断断四边形CDAN是平行四边形;
(3)存在.如图设T(x1,y1),Q(x2,y2),分别过T、Q作TF⊥y轴,QG⊥x轴,联立直线TQ解析式与抛物线解析式,可得x1,y1,x2,y2之间的关系,当以线段TQ为直径的圆恰好过坐标原点时,∠TOQ=90°,利用互余关系可证△TOF∽△QOG,利用相似比得出线段关系,结合x1,y1,x2,y2之间的关系求m的值.
试题解析:(1)A(-1,0)B(3,0)C(0,3).
(2)直线y=kx+t经过C、M两点,
所以![]()
即k=1,t=3,
直线解析式为y=x+3.
令y=0,得x=-3,
故D(-3,0),即OD=3,又OC=3,
∴在直角三角形COD中,根据勾股定理得:CD=![]() =
=![]() .
.
连接AN,过N做x轴的垂线,垂足为F.
设过A、N两点的直线的解析式为y=mx+n,
则![]() ,
,
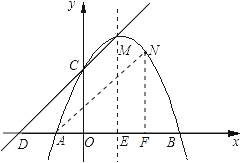
解得m=1,n=1
所以过A、N两点的直线的解析式为y=x+1
所以DC∥AN.在Rt△ANF中,AF=3,NF=3,
所以AN=![]() ,
,
所以DC=AN.
因此四边形CDAN是平行四边形.
(3)假设在x轴上方存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,设P(1,u)其中u>0,
则PA是圆的半径且PA2=u2+22过P做直线CD的垂线,垂足为Q,则PQ=PA时以P为圆心的圆与直线CD相切.
由第(2)小题易得:△MDE为等腰直角三角形,故△PQM也是等腰直角三角形,
由P(1,u)得PE=u,PM=|4-u|,PQ=![]()
由PQ2=PA2得方程:![]() =u2+22,
=u2+22,
解得u=![]() ,舍去负值u=
,舍去负值u=![]() ,符合题意的u=
,符合题意的u=![]() ,
,
所以,满足题意的点P存在,其坐标为(1,![]() )
)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为
为![]() 边上的中点.
边上的中点.
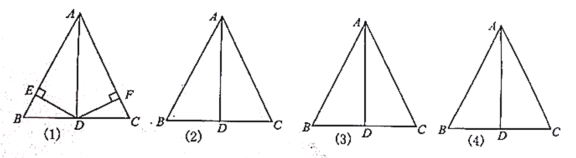
(1)若![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() .判断
.判断![]() 的形状,并证明;
的形状,并证明;
(2)若![]() 分别是
分别是![]() 上的中线,连接
上的中线,连接![]() .判断
.判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)若![]() 分别是
分别是![]() 的平分线,连接
的平分线,连接![]() .判断
.判断![]() 的关系,不需证明;
的关系,不需证明;
(4)若分别在![]() 上任取一点
上任取一点![]() ,且
,且![]() ,连接
,连接![]() .在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
.在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=8cm,如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为每秒2cm和1cm,FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t秒(0<t<4).
(1)连接EF,若运动时间t= 时,EF⊥AC;
(2)连接EP,当△EPC的面积为3cm2时,求t的值;
(3)若△EQP∽△ADC,求t的值.
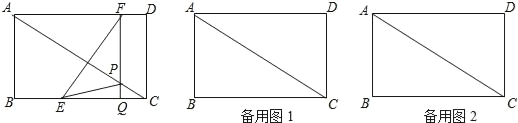
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国流传了上千年的传统节日,全国各地举行了丰富多彩的纪念活动,为了继承传统,减缓学生考前的心理压力,某班学生组织了一次拔河比赛,裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置,规则是:石头胜剪刀,剪刀胜布,布胜石头,手势相同则再决胜负.
(1)用列表或画树状图法,列出甲、乙两队手势可能出现的情况;
(2)裁判员的这种做法对甲、乙双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般成年人的脚长(厘米)与鞋码(码)有如下关系:
脚长 | 23 | 23.5 | 24 | 24.5 | … |
鞋码 | 36 | 37 | 38 | 39 | … |
(1)若某人的脚长为26厘米,他应穿多少码的鞋?
(2)请建立鞋码![]() (厘米)与脚长
(厘米)与脚长![]() (码)之间的函数表达式;
(码)之间的函数表达式;
(3)我国著名篮球运动员姚明穿53码的鞋,请你根据以上关系计算他的脚长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.
(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,
(1)证明:CF=EB.
(2)证明:AB=AF+2EB.
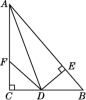
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com