
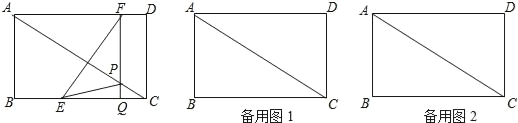
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=6cmЃЌBC=8cmЃЌШчЙћЕуEгЩЕуBГіЗЂбиBCЗНЯђЯђЕуCдШЫйдЫЖЏЃЌЭЌЪБЕуFгЩЕуDГіЗЂбиDAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЫќУЧЕФЫйЖШЗжБ№ЮЊУПУы2cmКЭ1cmЃЌFQЁЭBCЃЌЗжБ№НЛACЁЂBCгкЕуPКЭQЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈ0ЃМtЃМ4ЃЉЃЎ
ЃЈ1ЃЉСЌНгEFЃЌШєдЫЖЏЪБМфt=ЁЁ ЁЁЪБЃЌEFЁЭACЃЛ
ЃЈ2ЃЉСЌНгEPЃЌЕБЁїEPCЕФУцЛ§ЮЊ3cm2ЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉШєЁїEQPЁзЁїADCЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() УыЃЛЃЈ2ЃЉ2УыЃЛЃЈ3ЃЉ2Уы.
УыЃЛЃЈ2ЃЉ2УыЃЛЃЈ3ЃЉ2Уы.
ЁОНтЮіЁП
ЃЈ1ЃЉЯШШЗЖЈГіAC=10ЃЌНјЖјЕУГіЁЯACBЕФгрЯвжЕЃЌРћгУШ§НЧКЏЪ§ЕУГіCPЃЌCGЃЌМДПЩЕУГіPGЃЌдйХаЖЯГіЁїPFGЁзЁїEFQЃЌНЈСЂЗНГЬМДПЩЕУГіНсТлЃЌ
ЃЈ2ЃЉРћгУШ§НЧаЮЕФУцЛ§НЈСЂЗНГЬМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШХаЖЯГіEQ=CQЃЌНјЖјЕУГіCE=2CQЃЌНЈСЂЗНГЬМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌ
дкОиаЮABCDжаЃЌAB=6ЃЌBC=8ЃЌИљОнЙДЙЩЖЈРэЕУЃЌAC=10ЃЌ
ЁпЁЯB=ЁЯD=ЁЯBCD=90ЁуЃЌFQЁЭBCгкQЃЌ
ЁрЫФБпаЮCDFQЪЧОиаЮЃЌ
ЁрCQ=DFЃЌ
гЩдЫЖЏжЊЃЌBE=2tЃЌDF=tЃЌ
ЁрCQ=tЃЌCE=BCЉBE=8Љ2tЃЌAF=8ЉtЃЌ
ЁрEQ=CEЉCQ=8Љ3tЃЌ
дкRtЁїABCжаЃЌcosЁЯACB=![]() ЃЌ
ЃЌ
дкRtЁїCPQжаЃЌcosЁЯACB=![]() ,
,
ЁрCP=![]() tЃЌ
tЃЌ
ЁпEFЁЭACЃЌ
ЁрЁЯCGE=90Ёу=ЁЯABCЃЌ
ЁрЁЯACB+ЁЯFEQ=90ЁуЃЌ
ЁпЁЯACB+ЁЯBAC=90ЁуЃЌ
ЁрЁЯFEQ=ЁЯBACЃЌ
ЁрЁїABCЁзЁїEQFЃЎ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
ЁрEQ=![]() ЃЌ
ЃЌ
Ёр8Љ3t=![]() ЃЌ
ЃЌ
t=![]() УыЃЛ
УыЃЛ
ЙЪД№АИЪЧЃК![]() УыЃЛ
УыЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃЌCE=8Љ2tЃЌCQ=tЃЌ
дкRtЁїABCжаЃЌtanЁЯACB=![]() ЃЌ
ЃЌ
дкRtЁїCPQжаЃЌtanЁЯACB=![]() ЃЌ
ЃЌ
ЁрPQ=![]() tЃЌ
tЃЌ
ЁпЁїEPCЕФУцЛ§ЮЊ3cm2ЃЌ
ЁрSЁїEPC=![]() CEЁСPQ=
CEЁСPQ=![]() ЁСЃЈ8Љ2tЃЉЁС
ЁСЃЈ8Љ2tЃЉЁС![]() t=3ЃЌ
t=3ЃЌ
Ёрt=2УыЃЌ
МДЃКtЕФжЕЮЊ2УыЃЛ
ЃЈ3ЃЉЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрADЁЮBCЃЌ
ЁрЁЯCAD=ЁЯACBЃЌ
ЁпЁїEQPЁзЁїADCЃЌ
ЁрЁЯCAD=ЁЯQEPЃЌ
ЁрЁЯACB=ЁЯQEPЃЌ
ЁрEQ=CQЃЌ
ЁрCE=2CQЃЌ
гЩЃЈ1ЃЉжЊЃЌCQ=tЃЌCE=8Љ2tЃЌ
Ёр8Љ2t=2tЃЌ
Ёрt=2УыЃЎ
МДЃКtЕФжЕЮЊ2УыЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
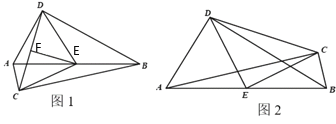
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌRtЁїABCКЭRtЁїABDжаЃЌЁЯACBЃНЁЯADBЃН90ЁуЃЌEЮЊABжаЕуЃЎ
ЃЈ1ЃЉШєСНИіжБНЧШ§НЧаЮЕФжБНЧЖЅЕудкABЕФвьВрЃЈШчЭМ1ЃЉЃЌСЌНгCDЃЌШЁCDжаЕуFЃЌСЌНгEFЁЂDEЁЂCEЃЌдђDEгыCEЪ§СПЙиЯЕЮЊ ЃЌEFгыCDЮЛжУЙиЯЕЮЊ ЃЛ
ЃЈ2ЃЉШєСНИіжБНЧШ§НЧаЮЕФжБНЧЖЅЕудкABЕФЭЌВрЃЈШчЭМ2ЃЉЃЌСЌНгCDЁЂDEЁЂCEЃЎ
ЂйШєЁЯCABЃН25ЁуЃЌЁЯDBAЃН35ЁуЃЌХаЖЯЁїDECЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЂкШєЁЯCAB+ЁЯDBAЃН![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊЖрЩйЖШЪБЃЌЁїDECЮЊЕШбќжБНЧШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ
ЮЊЖрЩйЖШЪБЃЌЁїDECЮЊЕШбќжБНЧШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШБп![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() Йигк
Йигк![]() жсЖдГЦЃЌ
жсЖдГЦЃЌ![]() НЛ
НЛ![]() жсИКАыжсгкЕу
жсИКАыжсгкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
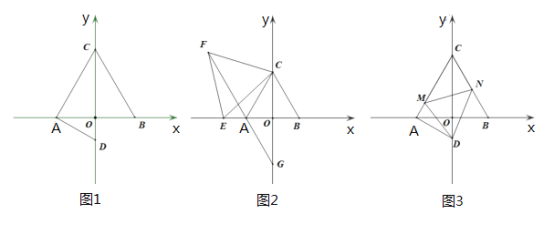
ЃЈ1ЃЉШчЭМ1ЃЌЧѓ![]() ЕузјБъЃЛ
ЕузјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌ![]() ЮЊ
ЮЊ![]() жсИКАыжсЩЯШЮвЛЕуЃЌвд
жсИКАыжсЩЯШЮвЛЕуЃЌвд![]() ЮЊБпзїЕШБп
ЮЊБпзїЕШБп![]() ЃЌ
ЃЌ![]() ЕФбгГЄЯпНЛ
ЕФбгГЄЯпНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌвд![]() ЮЊЖЅЕузї
ЮЊЖЅЕузї![]() ЕФНЧЃЌЫќЕФСНБпЗжБ№гы
ЕФНЧЃЌЫќЕФСНБпЗжБ№гы![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() КЭ
КЭ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎЬНОПЯпЖЮ
ЃЎЬНОПЯпЖЮ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() жЎМфЕФЙиЯЕЃЌВЂзгвджЄУїЃЎ
жЎМфЕФЙиЯЕЃЌВЂзгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌНЋвЛИіГЄЗНаЮжНЦЌ![]() биЖдНЧЯп
биЖдНЧЯп![]() елЕўЃЎЕу
елЕўЃЎЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌ
ДІЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌдђелЕўКѓжиКЯВПЗжЕФУцЛ§ЮЊЃЈ ЃЉ
ЃЌдђелЕўКѓжиКЯВПЗжЕФУцЛ§ЮЊЃЈ ЃЉ

A.6![]() B.8
B.8![]() C.10
C.10![]() D.12
D.12![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЕу![]() дке§БШР§КЏЪ§ЭМЯѓЩЯЃЌЕу
дке§БШР§КЏЪ§ЭМЯѓЩЯЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвдУПУы2ИіЕЅЮЛЕФЫйЖШгЩЕу
ЩЯвдУПУы2ИіЕЅЮЛЕФЫйЖШгЩЕу![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЕу
дЫЖЏЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯгЩЕу
ЩЯгЩЕу![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌ
дЫЖЏЃЌ![]() СНЕуЭЌЪБдЫЖЏЃЌЭЌЪБЭЃжЙЃЌдЫЖЏЪБМфЮЊ
СНЕуЭЌЪБдЫЖЏЃЌЭЌЪБЭЃжЙЃЌдЫЖЏЪБМфЮЊ![]() УыЃЎ
УыЃЎ
ЃЈ1ЃЉе§БШР§КЏЪ§ЕФЙиЯЕЪНЮЊ ЃЛ
ЃЈ2ЃЉЕБ![]() УыЃЌЧв
УыЃЌЧв![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉСЌНг![]() ЃЌдкЕу
ЃЌдкЕу![]() дЫЖЏЙ§ГЬжаЃЌ
дЫЖЏЙ§ГЬжаЃЌ![]() гы
гы![]() ЪЧЗёШЋЕШЃПШчЙћШЋЕШЃЌЧыЧѓГіЕу
ЪЧЗёШЋЕШЃПШчЙћШЋЕШЃЌЧыЧѓГіЕу![]() ЕФдЫЖЏЫйЖШЃЛШчЙћВЛШЋЕШЃЌЧыЫЕУїРэгЩЃЎ
ЕФдЫЖЏЫйЖШЃЛШчЙћВЛШЋЕШЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁКьАжАжДгМвЦяЕчЦПГЕГіЗЂЃЌбивЛЬѕжБТЗЕНЯрОр2400mЕФбЇаЃНгаЁКьЛиМвЃЌаЁКьАжАжГіЗЂЕФЭЌЪБЃЌаЁКьвд96m/minЕФЫйЖШДгбЇаЃбиЭЌвЛЬѕЕРТЗВНааЛиМвЃЌаЁКьАжАжИЯЕНбЇаЃаЃУХПкЕШКђ2minКѓжЊЕРаЁКьвбРыаЃЃЌСЂМДбидТЗвддЫйЗЕЛиЃЌЩшЫћУЧГіЗЂЕФЪБМфЮЊt minЃЌЭМЪОжаЕФелЯпOABDБэЪОаЁКьАжАжгыМвжЎМфЕФОрРыS1гыtжЎМфЕФКЏЪ§ЙиЯЕЃЌЯпЖЮEFБэЪОаЁКьгыМвжЎМфЕФОрРыS2гыtжЎМфЕФКЏЪ§ЙиЯЕЃЌдђаЁКьАжАжДгМвГіЗЂдкЗЕЛиЭОжазЗЩЯаЁКьЕФЪБМфЪЧЃЈ ЃЉ
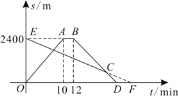
A.12minB.16minC.18minD.20min
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпЕФЖЅЕузјБъЮЊ![]() ЃЌЧвОЙ§Еу
ЃЌЧвОЙ§Еу![]() ЃЌгы
ЃЌгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() зѓВрЃЉЃЌгы
зѓВрЃЉЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
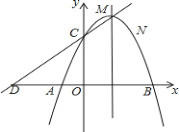
![]() ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
![]() ШєжБЯп
ШєжБЯп![]() ОЙ§
ОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЃЌЧвгы
СНЕуЃЌЧвгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЪджЄУїЫФБпаЮ
ЃЌЪджЄУїЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
![]() Еу
Еу![]() дкХзЮяЯпЕФЖдГЦжс
дкХзЮяЯпЕФЖдГЦжс![]() ЩЯдЫЖЏЃЌЧыЬНЫїЃКдк
ЩЯдЫЖЏЃЌЧыЬНЫїЃКдк![]() жсЩЯЗНЪЧЗёДцдкетбљЕФ
жсЩЯЗНЪЧЗёДцдкетбљЕФ![]() ЕуЃЌЪЙвд
ЕуЃЌЪЙвд![]() ЮЊдВаФЕФдВОЙ§
ЮЊдВаФЕФдВОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЃЌВЂЧвгыжБЯп
СНЕуЃЌВЂЧвгыжБЯп![]() ЯрЧаЃПШєДцдкЃЌЧыЧѓГіЕу
ЯрЧаЃПШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
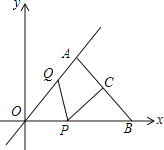
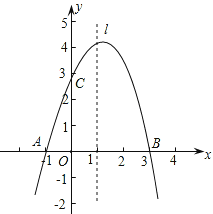
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2ЃЋbxЃЋcОЙ§A(Ѓ1ЃЌ0)ЁЂB(3ЃЌ0)ЁЂC(0ЃЌ3)Ш§ЕуЃЌжБЯпlЪЧХзЮяЯпЕФЖдГЦжсЃЎ
(1)ЧѓХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЩшЕуPЪЧжБЯпlЩЯЕФвЛИіЖЏЕуЃЌЕБЁїPACЕФжмГЄзюаЁЪБЃЌЧѓЕуPЕФзјБъЃЛ
(3)дкжБЯпlЩЯЪЧЗёДцдкЕуMЃЌЪЙЁїMACЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЫљгаЗћКЯЬѕМўЕФЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABC жаЃЌADЁЭBC гкЕу DЃЌЕу E ЮЊBDБпЩЯвЛЕуЃЌЙ§Еу E зї EGЁЮADЃЌЗжБ№НЛ AB КЭ CA ЕФбгГЄЯпгкЕу FЃЌGЃЌЁЯAFG=ЁЯGЃЎ

ЃЈ1ЃЉжЄУїЃКЁїABDЁеЁїACD
ЃЈ2ЃЉШєЁЯB=40ЁуЃЌжБНгаДГіЁЯFAG= Ёу
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com