
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌRtЁїABCКЭRtЁїABDжаЃЌЁЯACBЃНЁЯADBЃН90ЁуЃЌEЮЊABжаЕуЃЎ
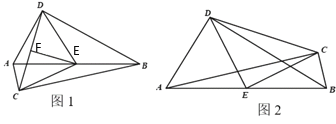
ЃЈ1ЃЉШєСНИіжБНЧШ§НЧаЮЕФжБНЧЖЅЕудкABЕФвьВрЃЈШчЭМ1ЃЉЃЌСЌНгCDЃЌШЁCDжаЕуFЃЌСЌНгEFЁЂDEЁЂCEЃЌдђDEгыCEЪ§СПЙиЯЕЮЊ ЃЌEFгыCDЮЛжУЙиЯЕЮЊ ЃЛ
ЃЈ2ЃЉШєСНИіжБНЧШ§НЧаЮЕФжБНЧЖЅЕудкABЕФЭЌВрЃЈШчЭМ2ЃЉЃЌСЌНгCDЁЂDEЁЂCEЃЎ
ЂйШєЁЯCABЃН25ЁуЃЌЁЯDBAЃН35ЁуЃЌХаЖЯЁїDECЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЂкШєЁЯCAB+ЁЯDBAЃН![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊЖрЩйЖШЪБЃЌЁїDECЮЊЕШбќжБНЧШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ
ЮЊЖрЩйЖШЪБЃЌЁїDECЮЊЕШбќжБНЧШ§НЧаЮЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЂйЕШБпШ§НЧаЮЃЌМћНтЮіЃЛЂк45ЁуЃЌРэгЩМћНтЮіЃЛ
ЃЛЃЈ2ЃЉЂйЕШБпШ§НЧаЮЃЌМћНтЮіЃЛЂк45ЁуЃЌРэгЩМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнжБНЧШ§НЧаЮЕФаББпжаЯпЕШгкаББпЕФвЛАыМДПЩЕУЕНDE=CEЃЌдйИљОнЕШбќШ§НЧаЮЕФШ§ЯпКЯвЛЕФаджЪМДПЩЕУЕНEFЁЭCDЃЛ
ЃЈ2ЃЉЂйЯШИљОнжБНЧШ§НЧаЮЕФаджЪЕУЕНЁїDECЪЧЕШбќШ§НЧаЮЃЌдйРћгУЭтНЧЕФаджЪЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌИљОнЦННЧЕФЖЈвхЧѓГіЁЯDECЃЌМДПЩЕУЕННсТлЃЛ
ЃЌИљОнЦННЧЕФЖЈвхЧѓГіЁЯDECЃЌМДПЩЕУЕННсТлЃЛ
ЂкгЩЂйЕУ![]() ЃЌDE=ECЃЌдйИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЧѓГіД№АИ.
ЃЌDE=ECЃЌдйИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЧѓГіД№АИ.
ЃЈ1ЃЉDE=CEЃЌEFЁЭCDЃЌ
ЁпЁїABDКЭЁїABCЪЧжБНЧШ§НЧаЮЃЌЁЯACBЃНЁЯADBЃН90ЁуЃЌEЮЊABжаЕуЃЌ
ЁрDE=![]() ABЃЌCE=
ABЃЌCE=![]() ABЃЌ
ABЃЌ
ЁрDE=CEЃЌ
ЁпЕуFЪЧCDЕФжаЕу,
ЁрEFЁЭCDЃЛ
ЃЈ2ЃЉЂйЁїDECЕШБпШ§НЧаЮЃЌ
дкRtЁїABCКЭRtЁїABDжаЃЌЁЯACBЃНЁЯADBЃН90ЁуЃЌEЮЊABжаЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЁїDECЪЧЕШбќШ§НЧаЮЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЧвЁЯDEAЁЂЁЯCEBЗжБ№ЪЧЁїDEBЁЂЁїAECЕФЭтНЧЃЌ
Ёр![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЁїDECЪЧЕШБпШ§НЧаЮЃЛ
ЂкгЩЂйЕУDE=EC,
![]() ЃЌ
ЃЌ
ЁпЁїDECЪЧЕШбќжБНЧШ§НЧаЮЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЮЊ45ЖШЪБЃЌЁїDECЮЊЕШбќжБНЧШ§НЧаЮ.
ЮЊ45ЖШЪБЃЌЁїDECЮЊЕШбќжБНЧШ§НЧаЮ.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМзЃЌввСНзщЪ§ОнЕФелЯпЭМШчЭМЫљЪОЃЌЩшМзЃЌввСНзщЪ§ОнЕФЗНВюЗжБ№ЮЊS2МзЃЌS2ввЃЌдђS2МзгыS2ввДѓаЁЙиЯЕЮЊЃЈЁЁЁЁЃЉ
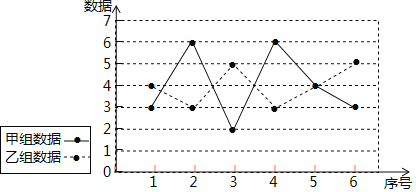
A.S2МзЃОS2ввB.S2МзЃНS2ввC.S2МзЃМS2ввD.ВЛФмШЗЖЈ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌДЙзуЗжБ№ЮЊ
ЃЌДЙзуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
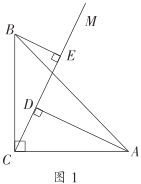
ЃЈ1ЃЉШчЭМ1ЃЌЂйЯпЖЮ![]() КЭ
КЭ![]() ЕФЪ§СПЙиЯЕЪЧ__________ЃЛ
ЕФЪ§СПЙиЯЕЪЧ__________ЃЛ
ЂкЧыаДГіЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕВЂжЄУїЃЎ
жЎМфЕФЪ§СПЙиЯЕВЂжЄУїЃЎ
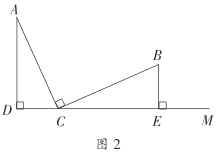
ЃЈ2ЃЉШчЭМ2ЃЌШєвбжЊЬѕМўВЛБфЃЌЩЯЪіНсТлЂкЛЙГЩСЂТ№ЃПШчЙћВЛГЩСЂЃЌЧыжБНгаДГіЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧаББп
ЪЧаББп![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№дкЯпЖЮ
ЗжБ№дкЯпЖЮ![]() ЃЌ
ЃЌ![]() ЩЯЃЌ Чв
ЩЯЃЌ Чв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЛ
ЮЊЕШбќжБНЧШ§НЧаЮЃЛ
ЃЈ2ЃЉШє![]() ЕФУцЛ§ЮЊ7ЃЌЧѓЫФБпаЮ
ЕФУцЛ§ЮЊ7ЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМЃЈ2ЃЉЃЌШчЙћЕу![]() дЫЖЏЕН
дЫЖЏЕН![]() ЕФбгГЄЯпЩЯЪБЃЌЕу
ЕФбгГЄЯпЩЯЪБЃЌЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЧвБЃГж
ЩЯЧвБЃГж![]() ЃЌ
ЃЌ![]() ЛЙЪЧЕШбќжБНЧШ§НЧаЮТ№ЃЎЧыЫЕУїРэгЩЃЎ
ЛЙЪЧЕШбќжБНЧШ§НЧаЮТ№ЃЎЧыЫЕУїРэгЩЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
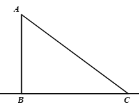
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌAB=3ЃЌBC=4ЃЌAC=5ЃЌдкжБЯпBCЩЯгаPЕуЃЌЪЙЁїPACЪЧвдACЮЊбќЕФЕШбќШ§НЧаЮЃЌдђBPЕФГЄЮЊ____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕШбќШ§НЧаЮЕФвЛИіЭтНЧЮЊ100ЁуЃЌдђетИіЕШбќШ§НЧаЮЕФЖЅНЧЮЊ________ЃЛЕШбќШ§НЧаЮвЛбќЩЯЕФИпгыбќЕФМаНЧЮЊ36ЁуЃЌдђИУЕШбќШ§НЧаЮЕФЖЅНЧЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() БпЩЯЕФжаЕуЃЎ
БпЩЯЕФжаЕуЃЎ
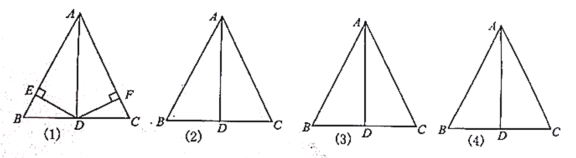
(1)Шє![]() гк
гк![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎХаЖЯ
ЃЎХаЖЯ![]() ЕФаЮзДЃЌВЂжЄУїЃЛ
ЕФаЮзДЃЌВЂжЄУїЃЛ
(2)Шє![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЩЯЕФжаЯпЃЌСЌНг
ЩЯЕФжаЯпЃЌСЌНг![]() ЃЎХаЖЯ
ЃЎХаЖЯ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
(3)Шє![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФЦНЗжЯпЃЌСЌНг
ЕФЦНЗжЯпЃЌСЌНг![]() ЃЎХаЖЯ
ЃЎХаЖЯ![]() ЕФЙиЯЕЃЌВЛашжЄУїЃЛ
ЕФЙиЯЕЃЌВЛашжЄУїЃЛ
(4)ШєЗжБ№дк![]() ЩЯШЮШЁвЛЕу
ЩЯШЮШЁвЛЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎдкВЛЬэМгИЈжњЯпЕФЧщПіЯТЃЌФуЛЙФмЕУЕНФФаЉВЛЭЌгкЩЯУцЕФе§ШЗНсТл?ЧыаДГіжСЩйЫФЬѕЃЌВЛашжЄУїЃЎ
ЃЎдкВЛЬэМгИЈжњЯпЕФЧщПіЯТЃЌФуЛЙФмЕУЕНФФаЉВЛЭЌгкЩЯУцЕФе§ШЗНсТл?ЧыаДГіжСЩйЫФЬѕЃЌВЛашжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкНјааЖўДЮИљЪНЛЏМђЪБЃЌЮвУЧгаЪБЛсХіЩЯШч![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() вЛбљЕФЪНзгЃЌетбљЕФЪНзгЮвУЧПЩвдНЋЦфНјвЛВНЛЏМђ
вЛбљЕФЪНзгЃЌетбљЕФЪНзгЮвУЧПЩвдНЋЦфНјвЛВНЛЏМђ![]() ЃН
ЃН![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() вдЩЯетжжЛЏМђЕФЗНЗЈНазіЗжФИгаРэЛЏЃЌЧыРћгУЗжФИгаРэЛЏНтД№ЯТСаЮЪЬтЃК
вдЩЯетжжЛЏМђЕФЗНЗЈНазіЗжФИгаРэЛЏЃЌЧыРћгУЗжФИгаРэЛЏНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЛЏМђЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєaЪЧ![]() ЕФаЁЪ§ВПЗжЃЌЧѓ
ЕФаЁЪ§ВПЗжЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉОиаЮЕФУцЛ§ЮЊ3![]() +1ЃЌвЛБпГЄЮЊ
+1ЃЌвЛБпГЄЮЊ![]() Љ2ЃЌЧѓЫќЕФжмГЄЃЎ
Љ2ЃЌЧѓЫќЕФжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
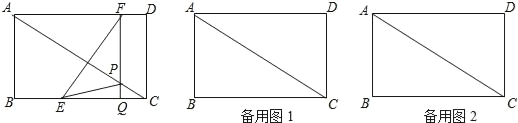
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=6cmЃЌBC=8cmЃЌШчЙћЕуEгЩЕуBГіЗЂбиBCЗНЯђЯђЕуCдШЫйдЫЖЏЃЌЭЌЪБЕуFгЩЕуDГіЗЂбиDAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЫќУЧЕФЫйЖШЗжБ№ЮЊУПУы2cmКЭ1cmЃЌFQЁЭBCЃЌЗжБ№НЛACЁЂBCгкЕуPКЭQЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈ0ЃМtЃМ4ЃЉЃЎ
ЃЈ1ЃЉСЌНгEFЃЌШєдЫЖЏЪБМфt=ЁЁ ЁЁЪБЃЌEFЁЭACЃЛ
ЃЈ2ЃЉСЌНгEPЃЌЕБЁїEPCЕФУцЛ§ЮЊ3cm2ЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉШєЁїEQPЁзЁїADCЃЌЧѓtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com