
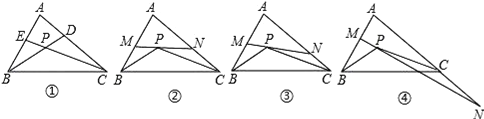
【题目】如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80,求∠BPC= .
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示) .
(3)将直线MN绕点P旋转。
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。

【答案】130°;
(2)90°﹣![]() ∠A
∠A
(3)(i)∠MPB+∠NPC=90°﹣![]() ∠A,理由见解析.
∠A,理由见解析.
(ii)不成立,有∠MPB﹣∠NPC=90°﹣![]() ∠A.
∠A.
理由见解析.
【解析】试题分析: (1)根据三角形内角和定理得到![]() ,再根据角平分线定义得到
,再根据角平分线定义得到![]() ,再利用三角形内角和定理得
,再利用三角形内角和定理得![]() ,然后把∠A的度数代入计算;
,然后把∠A的度数代入计算;
(2)根据平角定义得![]() ,然后根据(1)的求解;
,然后根据(1)的求解;
(3)( i)∠与(2)的说理一样;
(ⅱ)有结论![]() .
.
本题解析:(1) ![]()
![]()
![]()
![]()
![]() 故答案为:
故答案为: ![]()
(2)由![]() =
= ![]() 得∠MPB+∠NPC=
得∠MPB+∠NPC=![]() ∠BPC=
∠BPC=![]() 1(
1(![]() +
+![]() ∠A)=
∠A)= ![]()
![]() ∠A;故答案为:∠MPB+∠NPC=
∠A;故答案为:∠MPB+∠NPC=![]()
![]() ∠A.
∠A.
(3)(i)∠MPB+∠NPC=![]()
![]() ∠A.
∠A.
理由如下:
∵∠BPC=![]() +12∠
+12∠![]() A,
A,
∴∠MPB+∠NPC=![]() ∠BPC=180(
∠BPC=180(![]() +
+![]() ∠A)=
∠A)= ![]() 12
12![]() ∠A.
∠A.
(ii)不成立,有∠MPB∠NPC=![]()
![]() ∠A.
∠A.
理由如下:由题图④可知∠MPB+∠BPC∠NPC=![]() ,
,
由(1)知:∠BPC=![]() +
+![]() ∠A,∴∠MPB∠NPC=
∠A,∴∠MPB∠NPC=![]() ∠BPC=
∠BPC=![]() (
(![]() +
+![]() ∠A)=
∠A)= ![]()
![]() ∠A.
∠A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E在AD上,且EC平分∠BED。
(1)△BEC是否是等腰三角形?证明你的结论。
(2)若AB=1,∠ABE=450,求矩形ABCD的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个图案上各个点的横坐标和纵坐标分别加正数a,则所得的图案与原来图案相比( )
A.形状不变,大小扩大到原来的a倍
B.图案向右平移了a个单位
C.图案向上平移了a个单位
D.图案向右平移了a个单位,并且向上平移了a个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品进价a元,商店将价格提高30%作零售价销售,在销售旺季过后,商店以8折的价格开展促销活动,这时一件商品的售价为( )
A. a元 B. 1.04a元 C. 0.8a元 D. 0.92a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列正确结论的个数是( ) ①平行四边形内角和为360°;②平行四边形对角线相等;③平行四边形对角线互相平分;④平行四边形邻角互补.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B在数轴上对应的数分别用a、b表示,且(b+10)2+|a﹣20|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)当P点满足PB=2PA时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,依此类推,…点P能够移到与A、B重合的位置吗?若能,请探索第几次移动时重合;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com