
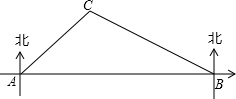
 如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=800m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}$≈1.732)
如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=800m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}$≈1.732) 科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}$=3$\sqrt{2}$ | B. | 3$\sqrt{2}$×2$\sqrt{3}$=6$\sqrt{6}$ | C. | ($\sqrt{5}$+1)2=6 | D. | ($\sqrt{7}$+2)($\sqrt{7}$-2)=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
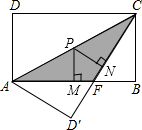 如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处.
如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,若⊙O的半径为10,AB是⊙O的一条弦,点C是⊙O上的一动点,且∠ACB=45°,点D、E分别是AC、BC的中点,直线DE与⊙O交于F、G两点.当DF+EG取得最大值时,弦BC的长为20.
如图,若⊙O的半径为10,AB是⊙O的一条弦,点C是⊙O上的一动点,且∠ACB=45°,点D、E分别是AC、BC的中点,直线DE与⊙O交于F、G两点.当DF+EG取得最大值时,弦BC的长为20.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com