
分析 (1)已知等式左边整理后,变形得到结果,原式化简后代入计算即可求出值;
(2)原式通分并利用同分母分式的减法法则变形,利用完全平方公式结合(1)的结果计算即可求出值.
解答 解:(1)已知等式整理得:$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{7}{a+b}$,即(a+b)2=7ab,
∴a2+b2=5ab,
(1)原式=$\frac{{a}^{2}+{b}^{2}}{ab}$=5;
(2)由$\frac{b}{a}$+$\frac{a}{b}$=5,两边平方得:($\frac{b}{a}$+$\frac{a}{b}$)2=$\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$+2=25,即$\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$=23,
∴($\frac{b}{a}$-$\frac{a}{b}$)2=$\frac{{b}^{2}}{{a}^{2}}$+$\frac{{a}^{2}}{{b}^{2}}$-2=21,
∵b>a>0,
∴$\frac{b}{a}$-$\frac{a}{b}$>0,
则$\frac{b}{a}$-$\frac{a}{b}$=$\sqrt{21}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
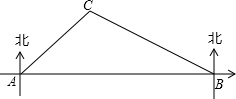 如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=800m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}$≈1.732)
如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=800m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
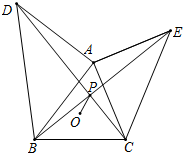 如图,已知△ABC,外心为O,BC=6,∠BAC=60°,分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE、CD交于点P,则OP的最小值是3-$\sqrt{3}$.
如图,已知△ABC,外心为O,BC=6,∠BAC=60°,分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE、CD交于点P,则OP的最小值是3-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com