
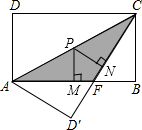
 如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处.
如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处.分析 (1)根据矩形的性质和翻折变换的性质得到AF=CF,设AF=x,根据勾股定理列出方程,解方程即可求出AF,根据三角形面积公式计算即可;
(2)连接PF,根据三角形的面积公式解答即可.
解答 解:(1)∵四边形ABCD是矩形,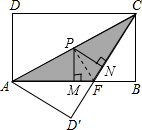
∴∠B=90°,AB∥CD,
∴∠DCA=∠BAC,
∵矩形沿AC折叠,点D落在点E处,
∴△ACD≌△ACE,
∴∠DCA=∠ECA,
∴∠BAC=∠ECA,
∴AF=CF,
设AF=CF=x,则BF=8-x,
在Rt△BCF中,根据勾股定理得:BC2+BF2=CF2,
即42+(8-x)2=x2,
解得:x=5,
∴AF=5,
∴S△ACF=$\frac{1}{2}$AF•BC=$\frac{1}{2}$×5×4=10;
(2)连接PF,
$\frac{1}{2}$×AF×PM+$\frac{1}{2}$×CF×PN=S△ACF=10,
∴PM+PN=4.
点评 本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:解答题
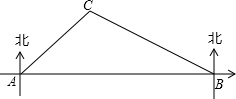 如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=800m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}$≈1.732)
如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=800m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com