
【题目】如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F. 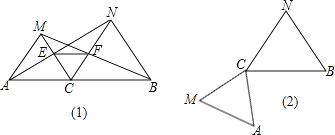
(1)求证:AN=MB;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由.
【答案】
(1)证明:∵△ACM,△CBN是等边三角形,
∴AC=MC,BC=NC,∠ACM=60°,∠NCB=60°,
在△CAN和△MCB中,
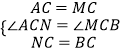 ,
,
∴△CAN≌△MCB(SAS),
∴AN=BM
(2)证明:∵△CAN≌△MCB,
∴∠CAN=∠CMB,
又∵∠MCF=180°﹣∠ACM﹣∠NCB=180°﹣60°﹣60°=60°,
∴∠MCF=∠ACE,
在△CAE和△CMF中,
 ,
,
∴△CAE≌△CMF(ASA),
∴CE=CF,
∴△CEF为等腰三角形,
又∵∠ECF=60°,
∴△CEF为等边三角形
(3)解:连接AN,BM,
∵△ACM、△CBN是等边三角形,
∴AC=MC,BC=CN,∠ACM=∠BCN=60°,
∵∠ACB=90°,
∴∠ACN=∠MCB,
在△ACN和△MCB中,
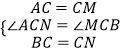 ,
,
∴△ACN≌△MCB(SAS),
∴AN=MB.
当把MC逆时针旋转90°后,AC也旋转了90°,因此∠ACB=90°,很显然∠FCE>90°,因此三角形FCE绝对不可能是等边三角形,
即结论1成立,结论2不成立.
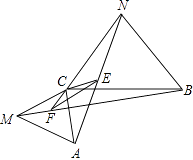
【解析】(1)可通过全等三角形来得出简单的线段相等,证明AN=BM,只要求出三角形ACN和MCB全等即可,这两个三角形中,已知的条件有AC=MC,NC=CB,只要证明这两组对应边的夹角相等即可,我们发现∠ACN和∠MCB都是等边三角形的外角,因此它们都是120°,这样就能得出两三角形全等了.也就证出了AN=BM.(2)我们不难发现∠ECF=180﹣60﹣60=60°,因此只要我们再证得两条边相等即可得出三角形ECF是等边三角形,可从EC,CF入手,由(1)的全等三角形我们知道,∠MAC=∠BMC,又知道了AC=MC,∠MCF=∠ACE=60°,那么此时三角形AEC≌三角形MCF,可得出CF=CE,于是我们再根据∠ECF=60°,便可得出三角形ECF是等边三角形的结论.(3)判定结论1是否正确,也是通过证明三角形ACN和BCM来求得.这两个三角形中MC=AC,NC=BC,∠MCB和∠ACN都是60°+∠ACB,因此两三角形就全等,AN=BM,结论1正确.如图,当把MC逆时针旋转90°后,AC也旋转了90°,因此∠ACB=90°,很显然∠FCE>90°,因此三角形FCE绝对不可能是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2![]() ,AE=8,则ED=______.
,AE=8,则ED=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B两个点.
(1)如图1,若AB=a,M是AB的中点,C为线段AB上的一点,且![]() ,则AC= ,CB= ,MC= (用含a的代数式表示);
,则AC= ,CB= ,MC= (用含a的代数式表示);
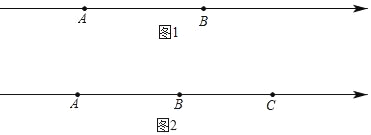
(2)如图2,若A、B、C三点对应的数分别为﹣40,﹣10,20.
①当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段AB的中点,点N为线段BC的中点,在B、C相遇前,在运动多少秒时恰好满足:MB=3BN.
②现有动点P、Q都从C点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到B点时,点Q才从C点出发,并以每秒3个单位长度的速度向左移动,且当点P到达A点时,点Q也停止移动(若设点P的运动时间为t).当PQ两点间的距离恰为18个单位时,求满足条件的时间t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店三、四月份出售同一品牌各种规格空调销售台输入下表,回答:
|
|
|
| |
三月 |
|
|
|
|
四月 |
|
|
|
|
![]() 商店平均每月销售空调________台;
商店平均每月销售空调________台;
![]() 商店出售各种规格的空调中,众数有________匹;
商店出售各种规格的空调中,众数有________匹;
![]() 在研究六月份进货时,商店经理决定________(匹)的空调要多进,________(匹)的空调要少进.
在研究六月份进货时,商店经理决定________(匹)的空调要多进,________(匹)的空调要少进.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABO中,AB⊥OB,OB= ![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为( ) 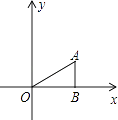
A.(﹣1, ![]() )
)
B.(﹣1, ![]() )或(﹣2,0)
)或(﹣2,0)
C.( ![]() ,﹣1)或(0,﹣2)
,﹣1)或(0,﹣2)
D.( ![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了完成“舌尖上的中国”的录制,节目组随机抽查了某省“A.奶制品类,B.肉制品类,C.面制品类,D.豆制品类”四类特色美食若干种,将收集的数据整理并绘制成下面两幅尚不完整的统计图,请根据图中信息完成下列问题:
(1)这次抽查了四类特色美食共 种,扇形统计图中a= ,扇形统计图中A部分圆心角的度数为 ;
(2)补全条形统计图;
(3)如果全省共有这四类特色美食120种,请你估计约有多少种属于“豆制品类”?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(﹣20);
(2)(﹣8)﹣(﹣1);
(3)|﹣10|+|+8|;
(4)(﹣12)﹣5+(﹣14)﹣(﹣39);
(5)0.47﹣4![]() ﹣(﹣1.53)﹣1
﹣(﹣1.53)﹣1![]() ;
;
(6)36﹣76+(﹣23)﹣105;
(7)﹣20+|﹣14|﹣(﹣18)﹣13;
(8)(+1.75)+(﹣![]() )+(+
)+(+![]() )+(+1.05)+(﹣
)+(+1.05)+(﹣![]() )+(+2.2).
)+(+2.2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣ ![]() x2+bx﹣6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
x2+bx﹣6的图象与x轴交于一点A(2,0),与y轴交于点B,对称轴与x轴交于点C,连接BA,BC,求△ABC的面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com