
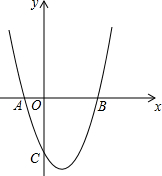
 如图,在平面直角坐标系中,点O是坐标原点,抛物线y=x2+bx+c与直线y=2x-6交于x轴正半轴上的B点,抛物线与x轴的负半轴交于点A,与y轴的负半轴交于点C,OB=3OA.
如图,在平面直角坐标系中,点O是坐标原点,抛物线y=x2+bx+c与直线y=2x-6交于x轴正半轴上的B点,抛物线与x轴的负半轴交于点A,与y轴的负半轴交于点C,OB=3OA.分析 (1)先根据一次函数解析式求出B点坐标,再利用OB=3OA得到A点坐标,然后利用交点式可得抛物线解析式;
(2)过点D作DH⊥x轴于H,如图1,先配方得到y=(x-1)2-4,则D(1,-4),再利用∠OCP+∠CDP=180°,∠OCP+∠1+∠DCP=180°得∠CDP=∠1+∠PCD,而由DH∥OC得到∠1=∠CDH,所以∠PCD=∠HDB,然后在Rt△BDH中,利用正切的定义计算出tan∠HDB=$\frac{BH}{DH}$=$\frac{1}{2}$,从而得到tan∠PCD=$\frac{1}{2}$;
(3)分类讨论:当点F在射线CD上时,延长EF交y轴于M,过点D作DG⊥y轴于G,过点E作EK⊥y轴于K,如图2,易得C(0,-3),则CG=DG=1,△DCG为等腰直角三角形,所以∠DCG=45°,易得△CMF和△MEK都是等腰直角三角形;由②得tan∠CEF=tan∠DCP=$\frac{1}{2}$,若设CF=a,则EF=2a,MF=a,EM=3a,根据等腰直角三角形的性质得KM=KE=$\frac{3\sqrt{2}}{2}$a,CM=$\sqrt{2}$CF=$\sqrt{2}$a,则OK=OM-KM=OC+CM-KM=3-$\frac{\sqrt{2}}{2}$a,于是可表示出E($\frac{3\sqrt{2}}{2}$a,$\frac{\sqrt{2}}{2}$a-3),利用二次函数图象上点的坐标特征得($\frac{3\sqrt{2}}{2}$a)2-2•$\frac{3\sqrt{2}}{2}$a-3=$\frac{\sqrt{2}}{2}$a-3,解得a1=0(舍去),a2=$\frac{7\sqrt{2}}{9}$,于是得到E($\frac{7}{3}$,-$\frac{20}{9}$);当点F在线段DC的延长线上时,用同样方法得E($\frac{\sqrt{2}}{2}$a,$\frac{3\sqrt{2}}{2}$a-3),把E点坐标代入抛物线解析式得($\frac{\sqrt{2}}{2}$a)2-2•$\frac{\sqrt{2}}{2}$a-3=$\frac{3\sqrt{2}}{2}$a-3,则可解得a1=0(舍去),a2=5$\sqrt{2}$,易得E(5,12),所以综上所述,E点坐标为($\frac{7}{3}$,-$\frac{20}{9}$)或(5,12).
解答 解:(1)当y=0时,2x-6=0,解得x=3,则B(3,0),
∵OB=3OA,
∴OA=1,
∴A(-1,0),
∴抛物线解析式为y=(x+1)(x-3)=x2-2x-3;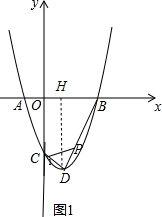 (2)过点D作DH⊥x轴于H,如图1,
(2)过点D作DH⊥x轴于H,如图1,
∵y=x2-2x-3=(x-1)2-4,
∴D(1,-4),
∴DH=4,OH=1,
∵∠OCP+∠CDP=180°,
而∠OCP+∠1+∠DCP=180°,
∴∠CDP=∠1+∠PCD,
∴DH∥OC,
∴∠1=∠CDH,
∴∠PCD=∠HDB
在Rt△BDH中,tan∠HDB=$\frac{BH}{DH}$=$\frac{3-1}{4}$=$\frac{1}{2}$,
∴tan∠PCD=$\frac{1}{2}$;
(3)当点F在射线CD上时,延长EF交y轴于M,过点D作DG⊥y轴于G,过点E作EK⊥y轴于K,如图2,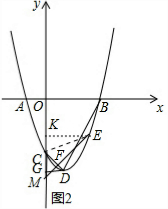
当x=0时,y=x2-2x-3=-3,则C(0,-3),
∵CG=OG-OC=4-3=1,DG=1,
∴CG=DG,
∴△DCG为等腰直角三角形,
∴∠DCG=45°,
∵EF⊥CD,
∴∠CMF=45°,
∴△CMF和△MEK都是等腰直角三角形,
由②得tan∠CEF=tan∠DCP=$\frac{1}{2}$,
设CF=a,则EF=2a,MF=a,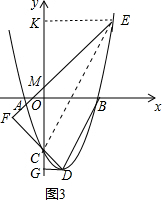
∴EM=3a,
∴KM=KE=$\frac{\sqrt{2}}{2}$EM=$\frac{3\sqrt{2}}{2}$a,CM=$\sqrt{2}$CF=$\sqrt{2}$a,
∵OK=OM-KM=OC+CM-KM=3+$\sqrt{2}$a-$\frac{3\sqrt{2}}{2}$a=3-$\frac{\sqrt{2}}{2}$a,
∴E($\frac{3\sqrt{2}}{2}$a,$\frac{\sqrt{2}}{2}$a-3),
∴E点在抛物线y=x2-2x-3上,
∴($\frac{3\sqrt{2}}{2}$a)2-2•$\frac{3\sqrt{2}}{2}$a-3=$\frac{\sqrt{2}}{2}$a-3,
整理得9a2-7$\sqrt{2}$a=0,解得a1=0(舍去),a2=$\frac{7\sqrt{2}}{9}$,
∴E($\frac{7}{3}$,-$\frac{20}{9}$)
当点F在线段DC的延长线上时,同样方法可得E($\frac{\sqrt{2}}{2}$a,$\frac{3\sqrt{2}}{2}$a-3),
∴E点在抛物线y=x2-2x-3上
∴($\frac{\sqrt{2}}{2}$a)2-2•$\frac{\sqrt{2}}{2}$a-3=$\frac{3\sqrt{2}}{2}$a-3,
整理得a2-5$\sqrt{2}$a=0,解得a1=0(舍去),a2=5$\sqrt{2}$,
∴E(5,12).
综上所述,E点坐标为($\frac{7}{3}$,-$\frac{20}{9}$)或(5,12).
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰直角三角形的判定与性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质;会解一元二次方程.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
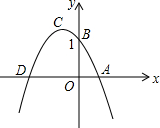 如图是二次函数y=mx2+nx+b的图象,已知它的顶点C在第二象限,且经过点A(1,0),点B(0,1),与x轴另一交点为D,当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时,m的值为( )
如图是二次函数y=mx2+nx+b的图象,已知它的顶点C在第二象限,且经过点A(1,0),点B(0,1),与x轴另一交点为D,当△ACD的面积为△ABD面积的$\frac{3}{2}$倍时,m的值为( )| A. | $\sqrt{3}$-2 | B. | -2±$\sqrt{3}$ | C. | 2-$\sqrt{3}$ | D. | -2-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
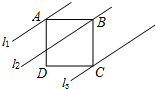 如图,已知正方形ABCD,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为3,l2与l3的距离为5,则正方形ABCD的面积等于( )
如图,已知正方形ABCD,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为3,l2与l3的距离为5,则正方形ABCD的面积等于( )| A. | 9 | B. | 25 | C. | 34 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com