
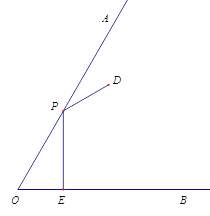
【题目】如图,已知∠AOB=60°,点P为射线OA上的一个动点,过点P作PE⊥OB,交OB 于点E,点D在∠AOB内,且满足∠DPA=∠OPE,DP+PE=6.
(1)当DP=PE时,求DE的长;
(2)在点P的运动过程中,请判断是否存在一个定点M,使得![]() 的值不变?并证明你的判断.
的值不变?并证明你的判断.
【答案】(1)DE=3![]() ;(2)当M点在射线OA上且满足OM=2
;(2)当M点在射线OA上且满足OM=2![]() 时,
时,![]() 的值不变,始终为1.理由见解析.
的值不变,始终为1.理由见解析.
【解析】
(1)作PF⊥DE交DE于F.由直角三角形的两锐角互余得到∠OPE=30°,在由平角的定义,得出∠EPD=120°.然后解三角形DPE即可得出结论.
(2)当点P与点M不重合时,延长EP到K使得PK=PD.可以证明△KPM≌△DPM,得到MK=MD.作ML⊥OE于L,MN⊥EK于N.解Rt△MLO得到ML的长,易证四边形MNEL为矩形,得到EN=ML=3.通过证明MK=ME,得到ME=MK=MD,即可得到![]() =1.
=1.
当点P与点M重合时,结论也成立.
(1)作PF⊥DE交DE于F.
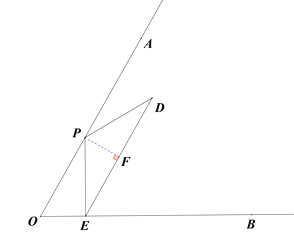
∵PE⊥BO,∠AOB=60°,∴∠OPE=30°,∴∠DPA=∠OPE=30°,∴∠EPD=120°.
∵DP=PE,DP+PE=6,∴∠PDE=30°,PD=PE=3,∴DF=PDcos30°=![]() ,∴DE=2DF=
,∴DE=2DF=![]() .
.
(2)当M点在射线OA上且满足OM=![]() 时,
时,![]() 的值不变,始终为1.理由如下:
的值不变,始终为1.理由如下:
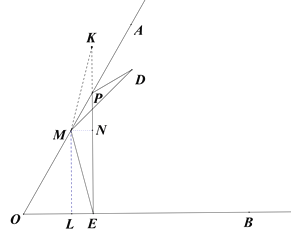
①当点P与点M不重合时,延长EP到K使得PK=PD,连接MK.
∵∠DPA=∠OPE,∠OPE=∠KPA,∴∠KPA=∠DPA,∴∠KPM=∠DPM.
∵PK=PD,PM是公共边,∴△KPM≌△DPM,∴MK=MD.
作ML⊥OE于L,MN⊥EK于N.
∵MO=![]() ,∠MOL=60°,∴ML=MOsin60°=3.
,∠MOL=60°,∴ML=MOsin60°=3.
∵PE⊥BO,ML⊥OE,MN⊥EK,∴四边形MNEL为矩形,∴EN=ML=3.
∵EK=PE+PK=PE+PD=6,∴EN=NK.
∵MN⊥EK,∴MK=ME,∴ME=MK=MD,即![]() =1.
=1.
②当点P与点M重合时,由上述过程可知结论成立.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为2,作正方形AEFG(A,E,F,G四个顶点按逆时针方向排列),连接BE、GD,
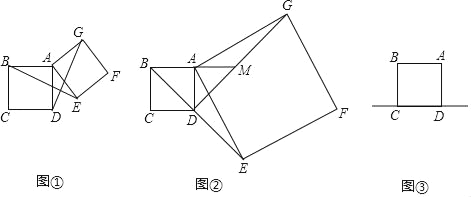
(1)如图①,当点E在正方形ABCD外时,线段BE与线段DG有何关系?直接写出结论;
(2)如图②,当点E在线段BD的延长线上,射线BA与线段DG交于点M,且DG=2DM时,求边AG的长;
(3)如图③,当点E在正方形ABCD的边CD所在的直线上,直线AB与直线DG交于点M,且DG=4DM时,直接写出边AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:⑴⑵的计算结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学艺术节期间,学校向学生征集书画作品,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(1)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请你将条形统计图补充完整,并估计全校共征集多少件作品?
(3)如果全校征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知已知抛物线经过原点O和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
(1)求m的值及该抛物线的解析式
(2)P(x,y)是抛物线上的一点,若S△ADP=S△ADC,求出所有符合条件的点P的坐标.
(3)点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形?若能,请直接写出点M的运动时间t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
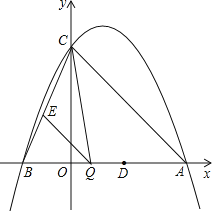
【题目】已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)求该二次函数的关系式;
(2)写出该二次函数的对称轴和顶点坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
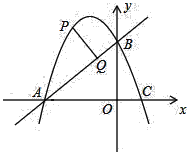
【题目】如图,已知二次函数y=﹣x2+bx+3的图象与x轴交于A、C两点(点A在点C的左侧),与y轴交于点B,且OA=OB.
(1)求线段AC的长度;
(2)若点P在抛物线上,点P位于第二象限,过P作PQ⊥AB,垂足为Q.已知PQ=![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com