
分析 (1)三个数-1,3,0最大的数是3,三个数2,x2+2,x+1中,x<0时,最大的数是x2+2;
(2)三个数x-1,5-4x,3x+2的平均数是2,根据题意得出$\left\{\begin{array}{l}{2x+2≥2}\\{4-2x≥2}\end{array}\right.$,解不等式组即可求得;
(3)三个数2,x+1,2x的平均数与最大数相等.
解答 解:(1)∵-1,3,0最大的数是3,
∴max{-1,3,0}=3,
∵若x<0,2,x2+2,x+1中,最大的数是x2+2,
∴max{2,x2+2,x+1}=x2+2;
故答案为3,x2+2;
(2)∵M(x-1,5-4x,3x+2}=2,
∴$\left\{\begin{array}{l}{2x+2≥2}\\{4-2x≥2}\end{array}\right.$,
则0≤x≤1.
(3)∵M{x2-4x-5,x2+7x-7}=x2+$\frac{3}{2}$x-6,
令12-x=2x-6,
∴x=6,
当x=6时,12-x=2x-6=6,
∴max{12-x,2x-6,6}=6,
则$\frac{2}{3}$x2+x=6,
∴x1=$\frac{-3+\sqrt{153}}{4}$,x2=$\frac{-3-\sqrt{153}}{4}$,
当x>6时,2x-6>6>12-x,
∴max{12-x,2x-6,6}=2x-6,则$\frac{2}{3}$x2+x=2x-6,无解;
当x<6时,12-x>6>2x-6,
∴max{12-x,2x-6,6}=12-x
则$\frac{2}{3}$x2+x=12-x,
∴x1=-6,x2=3.
点评 本题考查了一元一次不等式组的应用.解题的关键是弄清新定义运算的法则.


科目:初中数学 来源: 题型:选择题
| A. | 1m | B. | 9m | C. | 3m | D. | 13m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
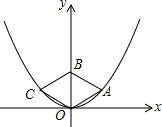 如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )
如图,菱形OABC的顶点O、A、C在抛物线y=$\frac{1}{3}$x2上,其中点O为坐标原点,对角线OB在y轴上,且OB=2.则菱形OABC的面积是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
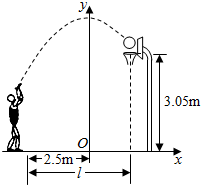 在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )
在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )| A. | 3.5m | B. | 4m | C. | 4.5m | D. | 4.6m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com