
【题目】如图,已知二次函数y=![]() x2+
x2+![]() x﹣
x﹣![]() 的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
(1)求抛物线顶点 D 的坐标以及直线 AC 的函数表达式;
(2)点 P 是抛物线上一点,且点P在直线 AC 下方,点 E 在抛物线对称轴上,当△BCE 的周长最小时,求△PCE 面积的最大值以及此时点 P 的坐标;
(3)在(2)的条件下,过点 P 且平行于 AC 的直线分别交x轴于点 M,交 y 轴于点N,把抛物线y=![]() x2+
x2+![]() x﹣
x﹣![]() 沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.

【答案】(1)顶点D的坐标为(﹣1,﹣![]() ),直线AC的解析式为y=﹣
),直线AC的解析式为y=﹣![]() x﹣
x﹣![]() ;(2)当t=﹣
;(2)当t=﹣![]() 时,△PEC的面积最大,最大值是
时,△PEC的面积最大,最大值是![]() ,此时,点P的坐标为(﹣
,此时,点P的坐标为(﹣![]() ,﹣
,﹣![]() );(3)存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,D′点的坐标为(﹣1,
);(3)存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,D′点的坐标为(﹣1, ![]() )(﹣1,
)(﹣1, ![]() ),(﹣1,
),(﹣1, ![]() ),(﹣1,
),(﹣1, ![]() ).
).
【解析】试题分析:(1)根据配方法,可得顶点坐标,根据自变量与函数值的对应关系,可得答案,根据待定系数法,可得函数解析式;
(2)根据线段垂直平分线的性质,线段的性质,可得E的坐标,根据平行于y的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PQ,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;
(3)根据勾股定理,可得关于d的方程,根据解方程,可得答案.
试题解析:
(1)y=![]() x2+
x2+![]() x﹣
x﹣![]() =
=![]() (x+1)2﹣
(x+1)2﹣![]() ,顶点D的坐标为(﹣1,﹣
,顶点D的坐标为(﹣1,﹣![]() ),
),
当y=0时, ![]() x2+
x2+![]() x﹣
x﹣![]() =0,解得x1=﹣3,x2=1,
=0,解得x1=﹣3,x2=1,
∴A(﹣3,0),B(1,0).
当x=0时,y=﹣![]() ,
,
∴C(0,﹣![]() ),
),
∴直线AC的解析式为y=﹣![]() x﹣
x﹣![]()
(2)∵△CPE得周长为BC+CE+BE,其中BC的长是固定的,
∴周长取得最小值就是BE+CE取得最小值,
∵点E是抛物线对称轴上一点,
∴BE=AE,
∴BE+CE=AE+CE,
∴BE+CE的最小值是AC,点E是AC与对称轴的交点.
∴点E为(﹣1,﹣![]() ).
).
∵点P是抛物线上x轴下方一点,设点P为(t, ![]() t2+
t2+![]() t﹣
t﹣![]() ).且
).且![]() t2+
t2+![]() t﹣
t﹣![]() <0.
<0.
过点P作QP⊥x轴交直线AC于点Q,点Q坐标为(t,﹣![]() t﹣
t﹣![]() ).
).
当点p在对称轴左侧时,S△PCE=S△PCQ﹣S△PEQ=![]() PQ(0﹣t)﹣
PQ(0﹣t)﹣![]() PQ(﹣1﹣t)=
PQ(﹣1﹣t)=![]() PQ,
PQ,
当点P在对称轴的右侧时,S△PCE=S△PCQ+S△PEQ=![]() PQ(0﹣t)+
PQ(0﹣t)+![]() PQ[t﹣(﹣1)]=
PQ[t﹣(﹣1)]= ![]() PQ,
PQ,
∵PQ=(﹣![]() t﹣
t﹣![]() )﹣(
)﹣(![]() t2+
t2+![]() t﹣
t﹣![]() )=﹣
)=﹣![]() t2﹣
t2﹣![]() t,
t,
∴S△PCE=![]() PQ=﹣
PQ=﹣![]() t2﹣
t2﹣![]() t=﹣
t=﹣![]() (t+
(t+![]() )2+
)2+![]() .
.
当t=﹣![]() 时,△PEC的面积最大,最大值是
时,△PEC的面积最大,最大值是![]() ,此时,点P的坐标为(﹣
,此时,点P的坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)经过点P且平行于AC的直线MN的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
当x=0时,y=-![]() ,即N(0,﹣
,即N(0,﹣![]() ),当y=0时,x=﹣
),当y=0时,x=﹣![]() ,即M(﹣
,即M(﹣![]() ,0),
,0),
设点D′的坐标为(﹣1,d),则MN2=(﹣![]() )2+(﹣
)2+(﹣![]() )2=
)2=![]() ,MD′2=[﹣
,MD′2=[﹣![]() ﹣(﹣1)]2+d2=
﹣(﹣1)]2+d2=![]() +d2,ND′2=(﹣1)2+(﹣
+d2,ND′2=(﹣1)2+(﹣![]() ﹣d)2=d2+
﹣d)2=d2+![]() d+
d+![]() .
.
当∠MD′N=90°时,MD′2+ND′2=MN2,即![]() +d2+d2+
+d2+d2+![]() d+
d+![]() =
=![]() ,
,
整理,得4d2+7![]() d﹣17=0,解得d1=
d﹣17=0,解得d1=![]() ,d2=
,d2=![]() ,
,
当∠NMD′=90°时,MD′2=ND′2+MN2,即![]() +d2=d2+
+d2=d2+![]() d+
d+![]() +
+![]() ,
,
化简,得![]() d=﹣
d=﹣![]() ,解得d=﹣
,解得d=﹣![]() ,
,
当∠NMD′﹣90°时,ND′2=MD′2+MN2, ![]() 即d2+
即d2+![]() d+
d+![]() =
=![]() +d2+
+d2+![]() ,
,
化简,得![]() d=
d=![]() ,解得d=
,解得d=![]() ,
,
∴存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,D′点的坐标为(﹣1, ![]() )(﹣1,
)(﹣1, ![]() ),(﹣1,
),(﹣1, ![]() )(﹣1
)(﹣1![]() ).
).


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间,王老师计划组织朋友去晋西北游览两日.经了解,现有甲、乙两家旅行社针对组团两日游的游客报价均为每人500元,且提供的服务完全相同.甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按八折收费.假设组团参加甲、乙两家旅行社两日游的人数均为![]() 人.
人.
(1)请列式表示甲、乙两家旅行社收取组团两日游的总费用;
(2)若王老师组团参加两日游的人数共有30人,请你通过计算,在甲、乙两家旅行社中,帮助王老师选择收取总费用较少的一家.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一快递员需要在规定时间内开车将快递送到某地,若快递员开车每分钟行驶1.2![]() ,就早到10分钟;若快递员开车每分钟行驶0.8
,就早到10分钟;若快递员开车每分钟行驶0.8![]() ,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.
,就要迟到5分钟.试求出规定时间及快递员所行驶的总路程.
小明和小新在解答时先设出未知数,然后列出方程如下:
![]() ①,
①,![]() ②,其中方程①由小明所列,方程②由小新所列.
②,其中方程①由小明所列,方程②由小新所列.
(1)小明所设![]() 表示 ;
表示 ;
小新所设![]() 表示 .
表示 .
(2)请选小明或小新的方法写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④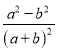 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()
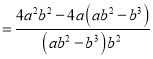
小强: ![]()
![]()
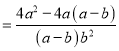
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,已知⊙O的直径为AB,AC⊥AB于点A, BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:①ED是⊙O的切线;②BC=2OE③△BOD为等边三角形;④△EOD ∽ △CAD,正确的是( )

A. ①② B. ②④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,某班同学用天平和一些物品(如图)探究了等式的基本性质.该班科技创新小组的同学提出问题:仅用一架天平和一个10克的砝码能否测量出乒乓球和一次性纸杯的质量?科技创新小组的同学找来足够多的乒乓球和某种一次性纸杯(假设每个乒乓球的质量相同,每个纸杯的质量也相同),经过多次试验得到以下记录:

记录 | 天平左边 | 天平右边 | 状态 |
记录一 | 6个乒乓球, 1个10克的砝码 | 14个一次性纸杯 | 平衡 |
记录二 | 8个乒乓球 | 7个一次性纸杯, 1个10克的砝码 | 平衡 |
请算一算,一个乒乓球的质量是多少克?一个这种一次性纸杯的质量是多少克?
解:(1)设一个乒乓球的质量是![]() 克,则一个这种一次性纸杯的质量是______克;(用含
克,则一个这种一次性纸杯的质量是______克;(用含![]() 的代数式表示)
的代数式表示)
(2)列一元一次方程求一个乒乓球的质量,并求出一个这种一次性纸杯的质量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)![]() 克糖水中有
克糖水中有![]() 克糖(
克糖(![]() >
>![]() >0),则糖的质量与糖水的质量比为_______;若再添加
>0),则糖的质量与糖水的质量比为_______;若再添加![]() 克糖,并全部溶解(
克糖,并全部溶解(![]() >0),则糖的质量与糖水的质量比为__________;生活常识告诉我们,添加的糖完全溶解后,糖水会更甜,因此我们可以猜想出以上两个质量比之间的大小关系是______________;
>0),则糖的质量与糖水的质量比为__________;生活常识告诉我们,添加的糖完全溶解后,糖水会更甜,因此我们可以猜想出以上两个质量比之间的大小关系是______________;
(2)我们的猜想正确吗?请你证明这个猜想。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com