
 如图,已知BC是⊙O的直径,点D为BC延长线上一点,点A为圆上一点,AB=AD,∠ADB=30°.
如图,已知BC是⊙O的直径,点D为BC延长线上一点,点A为圆上一点,AB=AD,∠ADB=30°. |
| AC |
 |
| AC |
 |
| AC |
| 60•π•2 |
| 180 |
| 2 |
| 3 |


科目:初中数学 来源: 题型:
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
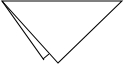 一位顾客在商店里挑选方台布时,他用了一种方法检验台布是否真的是正方形:拉起台布的一组对角,看是否对齐,(如图):在拉起另一组对角,看是否对齐,你认为这位顾客的检验方法正确吗?请说明理由.
一位顾客在商店里挑选方台布时,他用了一种方法检验台布是否真的是正方形:拉起台布的一组对角,看是否对齐,(如图):在拉起另一组对角,看是否对齐,你认为这位顾客的检验方法正确吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是一个浅湖的平面图,图中所有曲线都表示湖与岸边的分界线,如果P点在岸上,那么A点和B点分别在( )
如图是一个浅湖的平面图,图中所有曲线都表示湖与岸边的分界线,如果P点在岸上,那么A点和B点分别在( )| A、点A在水中,点B在水中 |
| B、点A在水中,点B在岸上 |
| C、点A在岸上,点B在水中 |
| D、点A在岸上,点B在岸上 |
查看答案和解析>>
科目:初中数学 来源: 题型:
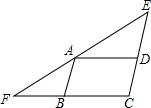 已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.
已知,如图,△EFC中,A是EF边上一点,AB∥EC,AD∥FC,若∠EAD=∠FAB,AB=a,AD=b.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com