
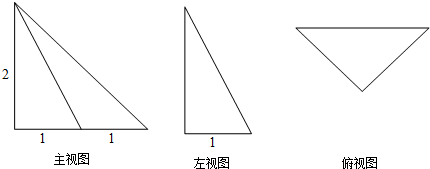
分析 由主视图知CD⊥平面ABC、B点在AC上的射影为AC中点及AC长,由左视图可知CD长及△ABC中变AC的高,利用勾股定理即可求出最长棱BD的长.
解答 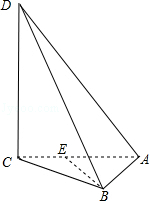 解:由主视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=1;
解:由主视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=1;
由主视图知CD=2,由左视图知BE=1,
在Rt△BCE中,BC=$\sqrt{2}$,
在Rt△BCD中,BD=$\sqrt{6}$,
在Rt△ACD中,AD=2$\sqrt{2}$.
则三棱锥中最长棱的长为2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查点、线、面间的距离计算,以及空间图形的三视图和学生的空间想象能力,关键是正确抽象出立体图形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
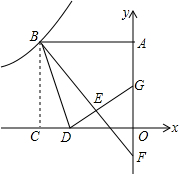 如图,正方形OABC的顶点A在y轴的正半轴上,顶点C在x轴的负半轴上,反比例函数y=-$\frac{9}{x}$在第二象限的图象经过点B,点D坐标为(-2,0),将正方形沿BD翻折,使点C落在E处,分别延长BE、DE角y轴于点F和G,则线段FG的长度是$\frac{5}{2}$.
如图,正方形OABC的顶点A在y轴的正半轴上,顶点C在x轴的负半轴上,反比例函数y=-$\frac{9}{x}$在第二象限的图象经过点B,点D坐标为(-2,0),将正方形沿BD翻折,使点C落在E处,分别延长BE、DE角y轴于点F和G,则线段FG的长度是$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我国二炮部队一批导弹的杀伤半径 | |
| B. | 了解中央电视台CCTV4《今日关注》栏目的收视率 | |
| C. | 了解射阳河流域中鱼的种类 | |
| D. | “勿忘国耻、振兴中华”!了解某班学生对我国政府设立“南京大屠杀国家公祭日”的知晓率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com