
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.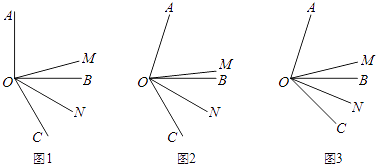
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
【答案】
(1)解:如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC= ![]() ∠AOC=75°,∠NOC=
∠AOC=75°,∠NOC= ![]() ∠BOC=30°
∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=45°.
(2)解:如图2,∠MON= ![]() α,
α,
理由是:∵∠AOB=α,∠BOC=60°,
∴∠AOC=α+60°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() α+30°,∠NOC=
α+30°,∠NOC= ![]() ∠BOC=30°
∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=( ![]() α+30°)﹣30°=
α+30°)﹣30°= ![]() α.
α.
(3)解:如图3,∠MON= ![]() α,与β的大小无关.
α,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC= ![]() ∠AOC=
∠AOC= ![]() (α+β),
(α+β),
∠NOC= ![]() ∠BOC=
∠BOC= ![]() β,
β,
∴∠AON=∠AOC﹣∠NOC=α+β﹣ ![]() β=α+
β=α+ ![]() β.
β.
∴∠MON=∠MOC﹣∠NOC
= ![]() (α+β)﹣
(α+β)﹣ ![]() β=
β= ![]() α
α
即∠MON= ![]() α.
α.
【解析】(1)由题意易求出∠AOC的度数,由OM平分∠AOC,ON平分∠BOC,可求得∠MOC和∠CON的度数,再由∠MON=∠MOC﹣∠NOC可求出;
(2)(3)解法同(1).


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得到的数据整理后,画出频数分布直方图(如图),图中从左到右依次为第1,2,3,4,5组.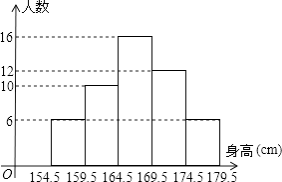
(1)求抽取了多少名男生测量身高?
(2)身高在哪个范围内的男生人数最多?(答出是第几小组即可)
(3)若该中学有300名男生,请估计身高为170cm及170cm以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.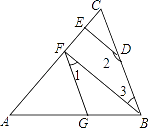
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6. 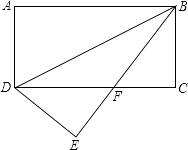
(1)求证:△EDF≌△CBF;
(2)求∠EBC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E、F.问四边形CFDE是正方形吗?请说明理由. 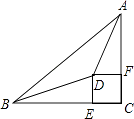
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形. 
(1)求证:AD=CE;
(2)猜想:AD和CE是否垂直?若垂直,请说明理由;若不垂直,则只要写出结论,不用写理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com