
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形. 
(1)求证:AD=CE;
(2)猜想:AD和CE是否垂直?若垂直,请说明理由;若不垂直,则只要写出结论,不用写理由.
【答案】
(1)解:∵△ABC和△DBE均为等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=∠CBE,
∴△ABD≌△CBE,
∴AD=CE.
(2)解:垂直.延长AD分别交BC和CE于G和F,

∵△ABD≌△CBE,
∴∠BAD=∠BCE,
∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,
又∵∠BGA=∠CGF,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.
【解析】(1)要证AD=CE,只需证明△ABD≌△CBE,由于△ABC和△DBE均为等腰直角三角形,所以易证得结论.(2)延长AD,根据(1)的结论,易证∠AFC=∠ABC=90°,所以AD⊥CE.
【考点精析】根据题目的已知条件,利用等腰直角三角形的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.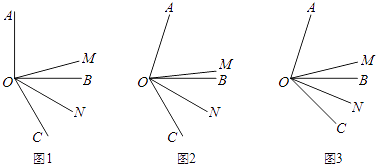
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点, N是BC的中点,则线段MN的长度是:( )
A.7cm
B.5cm或3cm
C.7cm或3cm
D.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
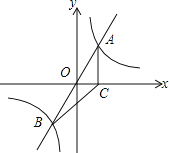
【题目】如图,直线y=mx与双曲线y=![]() 相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx>![]() 时,x的取值范围;
时,x的取值范围;
(3)在平面内是否存在一点D,使四边形ABDC为平行四边形?若存在,请求出点D坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA、OB分别是线段MC、MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短可为( ) 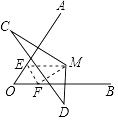
A.12cm
B.10cm
C.7cm
D.5cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com