
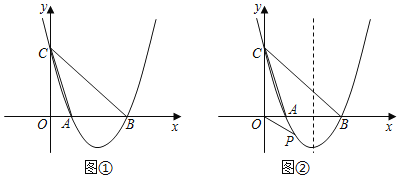
【题目】如图①,已知抛物线y=ax2﹣4amx+3am2(a、m为参数,且a>0,m>0)与x轴交于A、B两点(A在B的左边),与y轴交于点C.
(1)求点B的坐标(结果可以含参数m);
(2)连接CA、CB,若C(0,3m),求tan∠ACB的值;
(3)如图②,在(2)的条件下,抛物线的对称轴为直线l:x=2,点P是抛物线上的一个动点,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的的等腰直角三角形.若存在,求出所有符合条件的点P的坐标,若不存在,请说明理由.
【答案】(1)B(3m,0);(2)tan∠ACB=![]() ;
;
(3)点P的坐标是:(![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() ).
).
【解析】
(1)令y=0,解方程ax2﹣4amx+3am2=0,即可求出点B的坐标;
(2)过点A作AD⊥BC,垂足为点D,可得△BOC为等腰直角三角形,求出AD,CD,则tan∠ACB的值为![]() ;
;
(3)求出抛物线的解析式,分不同的情况:①当P在对称轴的左边,如图3,过P作MN⊥y轴,交y轴于M,交l于N,证明△OMP≌△PNF,根据|OM|=|PN|,列方程可得点P的坐标;同理可得其他图形中点P的坐标,②当P在对称轴的左边,过P作MN⊥x轴于N,过F作FM⊥MN于M,同理得△ONP≌△PMF,则可求出点P的坐标.
解:(1)令y=0,则有ax2﹣4amx+3am2=0,
解得:x1=m,x2=3m,
∵m>0,A在B的左边,
∴B(3m,0);
(2)如图1,过点A作AD⊥BC,垂足为点D,
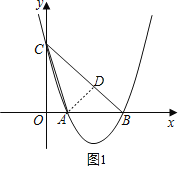
由(1)可知B(3m,0),则△BOC为等腰直角三角形,
∵OC=OB=3m,
∴BC=3![]() m,
m,
又∵∠ABC=45°,
∴∠DAB=45°,
∴AD=BD,
∵AB=2m,
∴![]() m,CD=2
m,CD=2![]() m,
m,
∴tan∠ACB=![]() ;
;
(3)∵由题意知x=2为对称轴,
∴2m=2,
即m=1,
∵在(2)的条件下有(0,3m),
∴3m=3am2,
解得m=![]() ,即a=1,
,即a=1,
∴抛物线的解析式为y=x2﹣4x+3,
①当P在对称轴的左边,如图2,过P作MN⊥y轴,交y轴于M,交l于N,
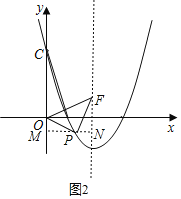
∵△OPF是等腰直角三角形,且OP=PF,
易得△OMP≌△PNF,
∴OM=PN,
∵P(m,m2﹣4m+3),
则﹣m2+4m﹣3=2﹣m,
解得:m=![]() 或
或![]() ,
,
∴P的坐标为(![]() ,
,![]() )或(
)或(![]() );
);
②当P在对称轴的右边,
如图3,过P作MN⊥x轴于N,过F作FM⊥MN于M,

同理得△ONP≌△PMF,
∴PN=FM,
则﹣m2+4m﹣3=m﹣2,
解得:x=![]() 或
或![]() ;
;
P的坐标为(![]() )或(
)或(![]() );
);
综上所述,点P的坐标是:(![]() )或(
)或(![]() )或(
)或(![]() )或(
)或(![]() ).
).


科目:初中数学 来源: 题型:
【题目】(问题提出)我们知道:同弧或等弧所对的圆周角都相等,且等于这条弧所对的圆心角的一半.那么,在一个圆内同一条弦所对的圆周角与圆心角之间又有什么关系?
(初步思考)(1)如图,![]() 是
是![]() 的弦,
的弦,![]() ,点
,点![]() 、
、![]() 分别是优弧
分别是优弧![]() 和劣弧
和劣弧![]() 上的点,则
上的点,则![]() ______°.
______°.![]() _______°.
_______°.

(2)如图,![]() 是
是![]() 的弦,圆心角
的弦,圆心角![]() ,点P是
,点P是![]() 上不与A、B重合的一点,求弦
上不与A、B重合的一点,求弦![]() 所对的圆周角
所对的圆周角![]() 的度数(用m的代数式表示).
的度数(用m的代数式表示).

(问题解决)(3)如图,已知线段![]() ,点C在
,点C在![]() 所在直线的上方,且
所在直线的上方,且![]() .用尺规作图的方法作出满足条件的点C所组成的图形(不写作法,保留作图痕迹).
.用尺规作图的方法作出满足条件的点C所组成的图形(不写作法,保留作图痕迹).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
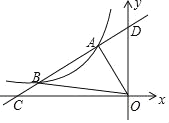
【题目】如图,直线y=kx+b与反比例函数![]() 的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.
的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.
(1)求此一次函数和反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中①所示的程序,得到了y与x的函数图象图中②,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P、Q,连结OP、OQ,则下列结论正确的是( )

A.△OPQ的面积为45
B.x<0时,![]()
C.x>0时,y随x的增大而增大
D.∠POQ可能等于90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我省深化课程改革以来,盘锦市某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
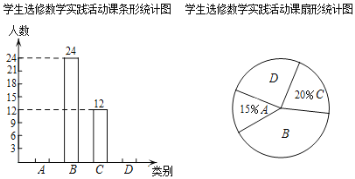
根据图中信息解决下列问题:
(1)本次共调查______名学生,扇形统计图中B所对应的扇形的圆心角为______度;
(2)补全条形统计图;
(3)该校参加实践活动课的学生共1200人,求该校参加D类实践活动课的学生大约多少人?
(4)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…n在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnn都是正方形,则正方形An﹣1BnAnn的周长为_____.
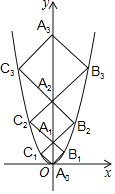
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ACB=90°,将AB边绕点B顺时针旋转90°得线段BD.过点D作DM⊥BC交BC延长线于M,
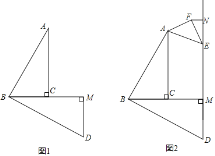
(1)如图1,请判断线段AC、CM、MD的数量关系并说明理由;
(2)E为DM延长线上一点,当点E为如图2所示的位置时,以AE为斜边向右侧作等腰Rt△AFE,再过点F作FN⊥DM于N,探究BM、FN、MN三条线段的数量关系,并说明理由;
(3)在问题(2)的条件下,当点E运动到某一位置时点B、A、F三点恰好在同一直线上,取DE中点P,连接AP,且AB=3,AF=1,请直接写出AP的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com