
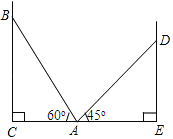
【题目】如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3![]() m.
m.
(1)求两面墙之间距离CE的大小;
(2)求点B到地面的垂直距离BC的大小.
【答案】(1)(3+3![]() )m;(2)点B到地面的垂直距离BC的大小3
)m;(2)点B到地面的垂直距离BC的大小3![]() m
m
【解析】
(1)在Rt△ADE中,运用勾股定理可求出梯子的总长度,然后利用勾股定理求得AC的长,从而求得线段CE的长;
(2)在Rt△ABC中,根据已知条件再次运用勾股定理可求出BC的长.
解:(1)在Rt△DAE中,
∵∠DAE=45°,
∴∠ADE=∠DAE=45°,AE=DE=3![]() m,
m,
∴AD2=AE2+DE2=36,
∴AD=6,即梯子的总长为6m.
∴AB=AD=6m.
在Rt△ABC中,∵∠BAC=60°,
∴∠ABC=30°,
∴AC=![]() AB=3m,
AB=3m,
∴CE=AC+AE=(3+3![]() )m;
)m;
(2)BC2=AB2﹣AC2=62﹣32=27,
∴BC=3![]() m,
m,
∴点B到地面的垂直距离BC的大小3![]() m.
m.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我国从2008年6月1日起执行“限塑令”.“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):
65,70,85,75,85,79,74,91,81,95.
(1)计算这10名学生所在家庭平均月使用塑料袋多少只?
(2)“限塑令”执行后,家庭月使用塑料袋数量预计将减少50%.根据上面的计算结果,估计该校1 000名学生所在家庭月使用塑料袋可减少多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
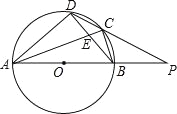
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=![]() 上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为
上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为![]() ,tan∠ABD=
,tan∠ABD=![]() ,则k的值为( )
,则k的值为( )

A. ﹣2 B. ﹣3 C. ﹣![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
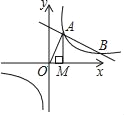
【题目】如图,一次函数y=﹣![]() x+
x+![]() 的图象与反比例函数y=
的图象与反比例函数y=![]() (k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要从甲.乙两名同学中选出一名,代表班级参加射击比赛,如图是两人最近10次射击训练成绩的折线统计图.
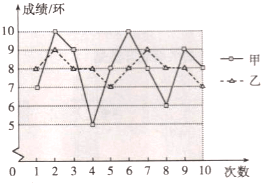
(1)已求得甲的平均成绩为8环,求乙的平均成绩;
(2)观察图形,直接写出甲,乙这10次射击成绩的方差![]() ,
, ![]() 哪个大;
哪个大;
(3)如果其他班级参赛选手的射击成绩都在7环左右,本班应该选 参赛更合适;如果其他班级参赛选手的射击成绩都在9环左右,本班应该选 参赛更合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 方格纸中小正方形的边长为1,
方格纸中小正方形的边长为1,![]() ,
,![]() 两点在格点上,要在图中格点上找到点
两点在格点上,要在图中格点上找到点![]() ,使得
,使得![]() 的面积为2,满足条件的点
的面积为2,满足条件的点![]() 有( )
有( )

A.无数个B.7个C.6个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰![]() 和等腰
和等腰![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() 交于点
交于点![]() .
.
(1)如图1,若![]() :
:
①![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
②![]() 的度数为 ;
的度数为 ;
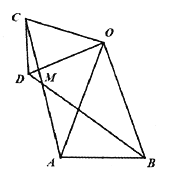
图1
(2)如图2,若![]() :
:
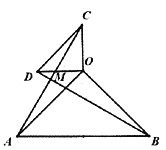
图2
①判断![]() 与
与![]() 之间存在怎样的数量关系?并说明理由;
之间存在怎样的数量关系?并说明理由;
②求![]() 的度数;
的度数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com