
 如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.
如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.| 1 |
| 2 |
| 1 |
| 2 |


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
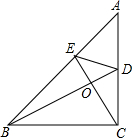 如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:
如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,如图,平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,取DE中点M并连接CM、BM.
已知,如图,平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,取DE中点M并连接CM、BM.查看答案和解析>>
科目:初中数学 来源: 题型:
 下图是一个长方形纸片,长为5a2+4b2,宽为6a2,在它的四个角上都剪去一个边长为
下图是一个长方形纸片,长为5a2+4b2,宽为6a2,在它的四个角上都剪去一个边长为| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … | ||||||||||
| 输出 | … |
|
|
|
|
| … |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AE是位于公路边的电线杆,高为12m,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).
如图,AE是位于公路边的电线杆,高为12m,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com