
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{{a}^{2}}$ |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
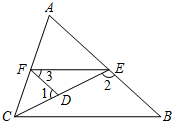 如图,已知∠1,∠2互为补角,且∠3=∠B,求证:∠AFE=∠ACB.
如图,已知∠1,∠2互为补角,且∠3=∠B,求证:∠AFE=∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}>\frac{a+c}{b+c}$ | B. | $\frac{a}{b}<\frac{a+c}{b+c}$ | C. | $\frac{a}{b}=\frac{a+c}{b+c}$ | D. | 前三种均有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
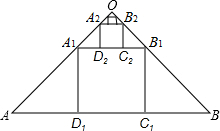 如图,在斜边长为1的等腰Rt△OAB中作内接正方形A1B1C1D1(正方形顶点都在△OAB边上),在等腰Rt△OA1B1中作内接正方形A2B2C2D2;在等腰Rt△OA2B2中,作内接正方形A3B3C3D3;…,依次作下去,则第5个正方形A5B5C5D5的边长为($\frac{1}{3}$)5.
如图,在斜边长为1的等腰Rt△OAB中作内接正方形A1B1C1D1(正方形顶点都在△OAB边上),在等腰Rt△OA1B1中作内接正方形A2B2C2D2;在等腰Rt△OA2B2中,作内接正方形A3B3C3D3;…,依次作下去,则第5个正方形A5B5C5D5的边长为($\frac{1}{3}$)5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com