
【题目】如图,AB为⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E点.
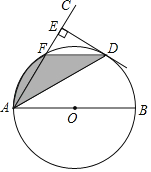
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=60°,求图中阴影部分的面积.
【答案】(1)见解析;(2)S阴影=![]() π.
π.
【解析】
(1)连接OD,先证明∠OAD=∠CAD,∠ODA=∠CAD,从而证明∠ODE=90°,即可证明DE是⊙O的切线;
(2)连接OF,根据∠BAC=60°和角度转换证明OD∥OC,即可证明S△AFD=S△AFO,把图中阴影部分面积转换得到扇形OAF的面积,再根据扇形面积公式即可求出.
解:(1)连结OD,
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵DE⊥AC,即∠AED=90°,
∴∠ODE=90°,即DE⊥OD,
∴DE是⊙O的切线;
(2)连接OF,
∵OD∥AC,
∴S△AFD=S△AFO,
∵∠BAC=60°,OA=OF,
∴△OAF为等边三角形,
∴∠AOF=60°,
∴S阴影=S扇形OAF=![]() =
=![]() π.
π.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
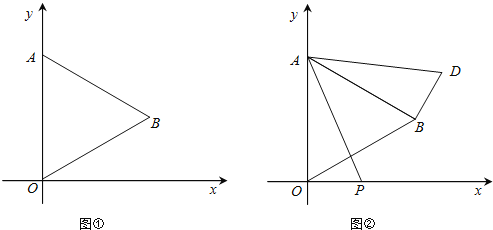
【题目】在平面直角坐标系中,已知点O为坐标原点,点A(0,4).△AOB是等边三角形,点B在第一象限.
(1)如图①,求点B的坐标;
(2)点P是x轴上的一个动点,连接AP,以点A为旋转中心,把△AOP逆时针旋转,使边AO与AB重合,得△ABD.
①如图②,当点P运动到点(![]() ,0)时,求此时点D的坐标;
,0)时,求此时点D的坐标;
②求在点P运动过程中,使△OPD的面积等于![]() 的点P的坐标(直接写出结果即可).
的点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种油菜籽在相同条件下的发芽试验结果如下表:
每批粒数n | 5 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 |
发芽粒数m | 4 | 9 | 60 | 116 | 282 | 639 | 1339 | 1806 | 2715 |
请用频率估计概率的方法来估计这批油菜籽在相同条件下的发芽概率是_______(精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
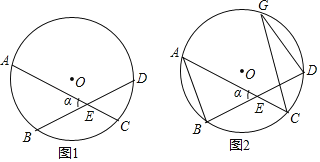
【题目】如图1,圆O的两条弦AC、BD交于点E,两条弦所成的锐角或者直角记为∠α
(1)点点同学通过画图和测量得到以下近似数据:
| 30.2° | 40.4° | 50.0° | 61.6° |
| 55.7° | 60.4° | 80.2° | 100.3° |
∠α的度数 | 43.0° | 50.2° | 65.0° | 81.0° |
猜想:![]() 、
、![]() 、∠α的度数之间的等量关系,并说明理由﹒
、∠α的度数之间的等量关系,并说明理由﹒
(2)如图2,若∠α=60°,AB=2,CD=1,将以![]() 圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
①求弦CG的长;
②求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形 OA1B1C1,依此方式,绕点O连续旋转2019次得到正方形OA2019B2019C2019,如果点A的坐标为(1,0),那么点B2019的坐标为( )
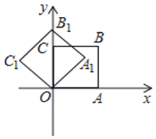
A.![]() B.
B.![]() C.(1,1)D.(﹣1,1)
C.(1,1)D.(﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点F,G,H分别是BE,CD,BC的中点
(1)观察猜想:图1中,△FGH的形状是______.
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△FGH的形状是否发生改变?并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=2,AB=6,请直接写出△FGH的周长的最大值.
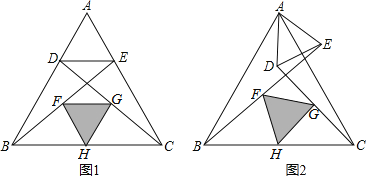
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com