
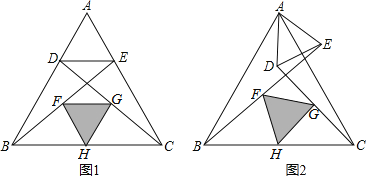
����Ŀ����ͼ1���ڵȱߡ�ABC�У���D��E�ֱ��ڱ�AB��AC�ϣ�AD��AE������BE��CD����F��G��H�ֱ���BE��CD��BC���е�
(1)�۲���룺ͼ1�У���FGH����״��______.
(2)̽��֤�����ѡ�ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã���FGH����״�Ƿ����ı䣿��˵�����ɣ�
(3)��չ���죺�ѡ�ADE�Ƶ�A��ƽ����������ת����AD��2��AB��6����ֱ��д����FGH���ܳ������ֵ.
���𰸡�(1)�ȱ������Σ�(2)�������ı䣬���ɼ�������(3)��PMN���ܳ������ֵΪ12.
��������
(1)�۲���룺
��ͼ1���ȸ��ݵȱ������ε����ʵõ�AB��AC����ABC����ACB��60������BD��CE���ٸ�����������λ�����ʵ�FH��CE��FH��![]() CE��GH��AD��GH��
CE��GH��AD��GH��![]() BD���Ӷ��õ�FH��GH����FHG��60�����Ӷ����ж���FGHΪ�ȱ������Σ�
BD���Ӷ��õ�FH��GH����FHG��60�����Ӷ����ж���FGHΪ�ȱ������Σ�
(2)̽��֤����
����CE��BD����ͼ2����������ת�Ķ��壬����ABD�Ƶ�A��ʱ����ת60���ɵõ���CAE����BD��CE����ABD����ACE����(1)һ���ɵ�FH��CE��FH��![]() CE��GH��AD��GH��
CE��GH��AD��GH��![]() BD���ɵ�FH��GH����BHF����BCE����CHG����CBD����������BHF+��CHG��120�����Ӷ��õ���FHG��60�������ǿ��ж���FHGΪ�ȱ�������.
BD���ɵ�FH��GH����BHF����BCE����CHG����CBD����������BHF+��CHG��120�����Ӷ��õ���FHG��60�������ǿ��ж���FHGΪ�ȱ�������.
(3)��չ���죺
����AB��AD��BD��AB+AD(���ҽ�����B��A��D����ʱȡ�Ⱥ�)�õ�BD�����ֵΪ8����GH�����ֵΪ4��Ȼ���ȷ����FHG���ܳ������ֵ.
�⣺(1)�۲���룺
��ͼ1���ߡ�ABCΪ�ȱ������Σ�
��AB��AC����ABC����ACB��60����
��AD��AE��
��BD��CE��
�ߵ�F��G��H�ֱ���BE��CD��BC���е�
��FH��CE��FH��![]() CE��GH��AD��GH��
CE��GH��AD��GH��![]() BD��
BD��
��FH��GH����BHF����BCA��60������CHG����CBA��60����
���FHG��60����
���FGHΪ�ȱ������Σ�
�ʴ�Ϊ���ȱ������Σ�
(2)̽��֤����
��PMN����״�������ı䣬��ȻΪ�ȱ�������.
�������£�����CE��BD����ͼ2��
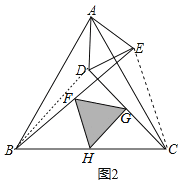
��AB��AC��AE��AD����BAC����DAE��60����
�����ABD�Ƶ�A��ʱ����ת60���ɵõ���CAE��
���ABD�ա�ACE��
��BD��CE����ABD����ACE��
��(1)һ���ɵ�FH��CE��FH��![]() CE��GH��AD��GH��
CE��GH��AD��GH��![]() BD��
BD��
��FH��GH����BHF����BCE����CHG����CBD��
���BHF+��CHG����BCE+��CBD����ABC����ABD+��ACB+��ACE��60��+60����120����
���FHG��60����
���FHGΪ�ȱ�������.
(3)��չ���죺
��GH��![]() BD��
BD��
�൱BD��ֵ���ʱ��GH��ֵ���
��AB��AD��BD��AB+AD(���ҽ�����B��A��D����ʱȡ�Ⱥ�)
��BD�����ֵΪ2+6��8��
��GH�����ֵΪ4��
���PMN���ܳ������ֵΪ12.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����AC���O���ڵ�F����ADƽ�֡�BAC��DE��AC������ΪE�㣮
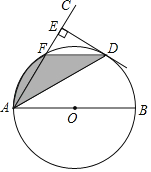
��1����֤��DE�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ2����BAC��60�㣬��ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֤�������ε���λ��ƽ���������εĵ����ߣ����ҵ��ڵ����ߵ�һ�룮���Ҫ�����£�
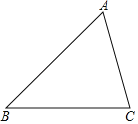
��1������ͼ�С�ABC���ó߹�����һ����λ��DE��������д��������Ӧ������ͼ�ۼ���
��2�����ݣ�1������������λ�ߣ�д����֪����֤��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
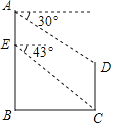
����Ŀ����ͼ������������AB��CD���60�ף��ӵ�A���D��ĸ���Ϊ30�㣬��A���½�10��E�㣬��E����C��ĸ���Ϊ43��������������ĸ߶ȣ�����ȷ��0.1�����ο����ݣ�![]() ��1.73��cos43���0.73��sin43���0.68��tan43���0.93��
��1.73��cos43���0.73��sin43���0.68��tan43���0.93��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�ⷽ�̣�x2��5��4x.
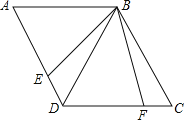
(2)��ͼ���ı���ABCD�У���C��60������BED��110����BD��BC����E��AD�ϣ���BE�Ƶ�B��ʱ����ת60����BF���ҵ�F��DC�ϣ����EBD�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+��2k��1��x+k2��0����������ʵ��x1��x2��
��1����ʵ��k��ȡֵ��Χ��
��2����������ʵ��x1��x2����x1+x2+x1x2��1��0����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��չ����������Ϊ�������ѧ����Ƴ��������ĸ���Ŀ��ѧ��ѡ��A��ģ���ʻ��B�����¾�����C�����絼�Σ�D��ֲ��ʶ��ѧУ�涨��ÿ��ѧ�������뱨����ֻ��ѡ������һ����Ŀ�����꼶��3�������������ʦ��ȫ��ѧ��ѡ�����Ŀ���������ͳ�ƣ�������������������������ͳ��ͼ������ͳ��ͼ�е���Ϣ������������⣺
��1�����꼶��3����ѧ������������ ������������ͳ��ͼ����������
��2������ʦ���ֱ����μ���ֲ��ʶ������ѧ����ǡ����������������������Щѧ����������ѡ�������λ��¼Ա�������б�����״ͼ�ķ�������ǡ��ѡ��1��������1��Ů�����λ��¼Ա�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����龳
��ͼ��ͬѧ���þ���ֽƬABCD��չ��ѧ̽���������AD=8��CD=6��
��������
��1����ͼ��1�����ֱ���BE,DF��ȥRt��ABE��Rt��CDF����ֽƬ�����ʣ���ֽƬBEDF���Σ���AE�ij���

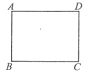
ͼ��1�� ͼ��2�� ͼ��3��
����̽��
�Ѿ���ֽƬABCD�ضԽ���AC�������õ���ABC��![]() ����ֽƬ
����ֽƬ
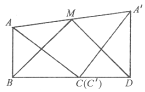
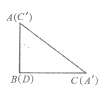
(2)������ֽƬ��ͼ��2���ڷţ���C��![]() �غϣ���B,C,D��ͬһ��ֱ���ϣ�����
�غϣ���B,C,D��ͬһ��ֱ���ϣ�����![]() ,��
,��![]() ���е�ΪM������BM��MD�����֦�BMD�ǵ��������Σ���֤����
���е�ΪM������BM��MD�����֦�BMD�ǵ��������Σ���֤����
��3����ͼ��3����������ֽƬ������һ��Ȼ��![]() ֽƬ�Ƶ�B˳ʱ����תa��00<a<900),����
ֽƬ�Ƶ�B˳ʱ����תa��00<a<900),����![]() ��
��![]() ��̽����ֱ��д���߶�
��̽����ֱ��д���߶�![]() ��
��![]() �Ĺ�ϵ��
�Ĺ�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com