
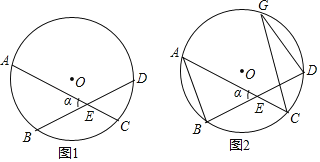
【题目】如图1,圆O的两条弦AC、BD交于点E,两条弦所成的锐角或者直角记为∠α
(1)点点同学通过画图和测量得到以下近似数据:
| 30.2° | 40.4° | 50.0° | 61.6° |
| 55.7° | 60.4° | 80.2° | 100.3° |
∠α的度数 | 43.0° | 50.2° | 65.0° | 81.0° |
猜想:![]() 、
、![]() 、∠α的度数之间的等量关系,并说明理由﹒
、∠α的度数之间的等量关系,并说明理由﹒
(2)如图2,若∠α=60°,AB=2,CD=1,将以![]() 圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点,连接CG﹒
①求弦CG的长;
②求圆O的半径.
【答案】(1)∠α=![]() (
(![]() 的度数+
的度数+![]() 的度数),见解析;(2)①
的度数),见解析;(2)①![]() ,②
,②![]()
【解析】
(1)连接BC,如图1,先利用三角形外角性质得到∠α=∠B+∠C,再利用圆周角与它所对弧的度数之间的关系得到∠B=![]() 的度数,∠C=
的度数,∠C=![]() 的度数,所以∠α=
的度数,所以∠α=![]() (
(![]() 的度数+
的度数+![]() 的度数);
的度数);
(2)①连接OG、OC、AG,作OH⊥CG于H,GF⊥CD于F,如图2,利用旋转的性质得![]() ,AB=DG=2,利用由(1)的结论得到
,AB=DG=2,利用由(1)的结论得到![]() 的度数为120°,则∠COG=120°,
的度数为120°,则∠COG=120°,
关键圆周角定理计算出∠CDG=120°,则∠GDF=60°,于是通过解直角三角形可计算出CG的长;
②利用垂径定理得到CH=GH=![]() ,然后通过解直角三角形求出OG即可.
,然后通过解直角三角形求出OG即可.
解:(1)∠α=![]() (
(![]() 的度数+
的度数+![]() 的度数)
的度数)
理由如下:连接BC,如图1,
∠α=∠B+∠C,
而∠B=![]() 的度数,∠C=
的度数,∠C=![]() 的度数,
的度数,
∴∠α=![]() (
(![]() 的度数+
的度数+![]() 的度数);
的度数);
(2)①连接OG、OC、AG,作OH⊥CG于H,GF⊥CD于F,如图2,
∵将![]() 以圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点G,
以圆心为中心顺时针旋转,直至点A与点D重合,同时B落在圆O上的点G,
∴![]() ,AB=DG=2,
,AB=DG=2,
由(1)得![]() 的度数+
的度数+![]() 的度数=2∠α=120°,
的度数=2∠α=120°,
![]() 的度数+
的度数+![]() 的度数=2∠α=120°,
的度数=2∠α=120°,
即![]() 的度数为120°,
的度数为120°,
∴∠COG=120°,
∴∠CAG=60°,
而∠CAG+∠CDG=120°,
∴∠CDG=120°,
∴∠GDF=60°,
在Rt△GDF中,DF=![]() DG=1,GF=
DG=1,GF=![]() DF=
DF=![]() ,
,
在Rt△CFG中,CG![]() ;
;
②∵OH⊥CG,
∴CH=GH=![]() CG=
CG=![]() ,
,
∵∠OGH=![]() (180°﹣120°)=30°,
(180°﹣120°)=30°,
∴![]() ,
,
∴OG=2OH=![]() ,
,
即圆O的半径为![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】某商家销售某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x元/件满足一次函数的关系,部分数据如下表:(![]() ,物价部门规定售价不得高于80元)
,物价部门规定售价不得高于80元)
销售单价x(元/件) | … | 55 | 60 | 65 | 70 | 75 |
一周的销售量y(件) | … | 450 | 400 | 350 | 300 | 250 |
(1)直接写出y与x的函数关系式:______;
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并求出销售利润的最大值;
(3)该商家要使每周的销售利润不低于5000元,那么销售单价应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=![]() x12的图象分别交x轴,y轴于A,C两点。
x12的图象分别交x轴,y轴于A,C两点。
(1)求出A,C两点的坐标;
(2)在x轴上找出点B,使△ACB∽△AOC,若抛物线过A,B,C三点,求出此抛物线的解析式;
(3)在(2)的条件下,设动点P、Q分别从A,B两点同时出发,以相同速度沿AC、BA向C,A运动,连接PQ,设AP=m,是否存在m值,使以A,P,Q为顶点的三角形与△ABC相似?若存在,求出所有m值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
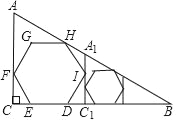
【题目】如图,Rt△ABC中,∠C=Rt∠,AB=2,∠B=30°,正六边形DEFGHI完全落在Rt△ABC内,且DE在BC边上,F在AC边上,H在AB边上,则正六边形DEFGHI的边长为_____,过I作A1C1∥AC,然后在△A1C1B内用同样的方法作第二个正六边形,按照上面的步骤继续下去,则第n个正六边形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E点.
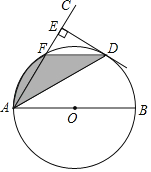
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱![]() 的长度;
的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O的半径为5cm,弦AB//CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
A. 1 cm B. 7cm C. 3 cm或4 cm D. 1cm 或7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:x2﹣5=4x.
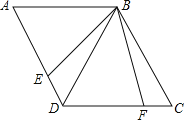
(2)如图,四边形ABCD中,∠C=60°,∠BED=110°,BD=BC,点E在AD上,将BE绕点B逆时针旋转60°得BF,且点F在DC上,求∠EBD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com