
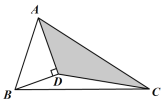
【题目】如图,AD平分∠BAC,BD⊥AD,垂足为D,连接CD,若三角形△ABC内有一点P,则点P落在△ADC内(包括边界的阴影部分)的概率为__________.
科目:初中数学 来源: 题型:
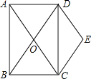
【题目】如图,矩形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 关于
关于![]() 的对称图形为
的对称图形为![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
①根据题意补全图形;
②若![]() =
=![]() ,请用等式表示线段
,请用等式表示线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b满足,![]() 且A(a,0)、B(0,b)
且A(a,0)、B(0,b)

(1) 如图,在x正半轴上有一点C(x,0).若△ABC的面积大于6,请直接写出x的取值范围____________;
(2)若在平面直角坐标系第四象限上存在一点N,N的坐标为(n,﹣n),满足4≤S△ABN≤8,求n的取值范围.
(3)若在平面直角坐标系上存在一点M,M的坐标为(m,﹣2m),请通过计算说明:无论m取何值△ABM的面积为定值,并求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为![]() .第一次操作:分别延长
.第一次操作:分别延长![]() ,
,![]() ,
,![]() 至点
至点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() ,顺次连接
,顺次连接![]() ,
,![]() ,
,![]() ,得到△
,得到△![]() .第二次操作:分别延长
.第二次操作:分别延长![]() ,
,![]() ,
,![]() 至点
至点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() ,顺次连接
,顺次连接![]() ,
,![]() ,
,![]() ,得到△
,得到△![]() ,…按此规律,要使得到的三角形的面积超过2020,最少经过多少次操作( )
,…按此规律,要使得到的三角形的面积超过2020,最少经过多少次操作( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN//EF, 点C 为两直线之间一点,若∠CAM 的平分线与∠CBF 的平分线所在的直线相交于点 D ,则∠ACB与 ∠ADB 之间的数量关系是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
① 20.2×19.8 ;
②![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料解决问题:
材料:古希腊著名数学家 毕达哥拉斯发现把数1,3,6,10,15,21…这些数量的(石子),都可以排成三角形,则称像这样的数为三角形数.
把数 1,3,6,10,15,21…换一种方式排列,即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
从上面的排列方式看,把1,3,6,10,15,…叫做三角形数“名副其实”.
(1)设第一个三角形数为a1=1,第二个三角形数为a2=3,第三个三角形数为a3=6,请直接写出第n个三角形数为an的表达式(其中n为正整数).
(2)根据(1)的结论判断66是三角形数吗?若是请说出66是第几个三角形数?若不是请说明理由.
(3)根据(1)的结论判断所有三角形数的倒数之和T与2的大小关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com