
【题目】如图,△ABC的面积为![]() .第一次操作:分别延长
.第一次操作:分别延长![]() ,
,![]() ,
,![]() 至点
至点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() ,顺次连接
,顺次连接![]() ,
,![]() ,
,![]() ,得到△
,得到△![]() .第二次操作:分别延长
.第二次操作:分别延长![]() ,
,![]() ,
,![]() 至点
至点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() ,顺次连接
,顺次连接![]() ,
,![]() ,
,![]() ,得到△
,得到△![]() ,…按此规律,要使得到的三角形的面积超过2020,最少经过多少次操作( )
,…按此规律,要使得到的三角形的面积超过2020,最少经过多少次操作( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
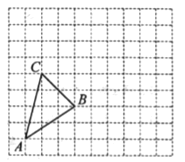
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=9,把矩形ABCD沿对角线BD折叠,使点C与点F重合,BF交AD于点M,过点C作CE⊥BF于点E,交AD于点G,则MG的长= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中,AB为⊙O的直径,AB=4,P为AB上一点,过点P作⊙O的弦CD,设∠BCD=m∠ACD.
(1)已知 ![]() ,求m的值,及∠BCD、∠ACD的度数各是多少?
,求m的值,及∠BCD、∠ACD的度数各是多少?
(2)在(1)的条件下,且 ![]() ,求弦CD的长;
,求弦CD的长;
(3)当 ![]() 时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由.
时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,∠BAC=90°
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD之间的位置关系为 , 数量关系为 .
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,为什么?
(2)如图4,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.且AC=4 ![]() ,BC=3,∠BCA=45°,正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,∠BCA=45°,正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD平分∠BAC,BD⊥AD,垂足为D,连接CD,若三角形△ABC内有一点P,则点P落在△ADC内(包括边界的阴影部分)的概率为__________.
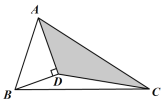
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )

A. 36 B. 12 C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.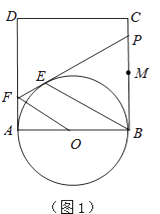
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(2,1),B(2,4).
(1)若直线l:y=x+b与AB有一个交点.

则b的取值范围为_______________;
(2)若直线l:y=kx与AB有一个交点.
则k的取值范围为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com