
【题目】图中,AB为⊙O的直径,AB=4,P为AB上一点,过点P作⊙O的弦CD,设∠BCD=m∠ACD.
(1)已知 ![]() ,求m的值,及∠BCD、∠ACD的度数各是多少?
,求m的值,及∠BCD、∠ACD的度数各是多少?
(2)在(1)的条件下,且 ![]() ,求弦CD的长;
,求弦CD的长;
(3)当 ![]() 时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由.
时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由.
【答案】
(1)解:如图1,
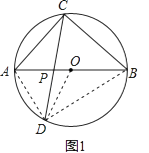
由 ![]() ,
,
得 m=2,
经检验m=2是原方程的根。
连结AD、BD
∵AB是⊙O的直径
∴∠ACB=90°,∠ADB=90°
又∵∠BCD=2∠ACD,∠ACB=∠BCD+∠ACD
∴∠ACD=30°,∠BCD=60°;
(2)解:如图1,连结AD、BD,则∠ABD=∠ACD=30°,AB=4
∴AD=2, ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∵∠APC=∠DPB,∠ACD=∠ABD
∴△APC∽△DPB
∴ ![]() ,
,
∴ACDP=APDB= ![]() ×2
×2 ![]() =
= ![]() ①,
①,
PCDP=APBP= ![]() ×
× ![]() =
= ![]() ②
②
同理△CPB∽△APD
∴ ![]() ,
,
∴BCDP=BPAD= ![]() ×2=
×2= ![]() ③,
③,
由①得 ![]() ,由③得
,由③得 ![]() ,
,
![]() ,
,
在△ABC中,AB=4,
∴ ![]() ,
,
∴ ![]()
由② ![]() ,
,
得 ![]()
∴ ![]()
方法二:由①÷③得 ![]() ,
,
在△ABC中,AB=4,AC= ![]() ×
× ![]() =
= ![]() ,
,
BC= ![]() ×2=
×2= ![]()
由③ ![]() ,
,
得 ![]()
由② ![]() ,
,
得 ![]()
∴ ![]() ;
;
(3)解:如图2,连结OD,
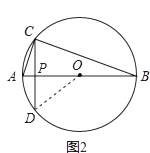
由 ![]() ,AB=4,
,AB=4,
则 ![]() ,
,
则 ![]() ,
,
则 ![]() ,
,
![]()
要使CD最短,则CD⊥AB于点P
于是 ![]() ,
,
∵∠POD=30°
∴∠ACD=15°,∠BCD=75°
∴m=5,故存在这样的m值,且m=5.
【解析】(1)先求出此分式方程的解,即可求出∠BCD=2∠ACD,连结AD、BD、OD,根据两圆周角所夹弧对的两圆心角之和为180°,即可求出∠BCD、∠ACD的度数,或根据直径所对的圆周角是直角,得到∠ACB=∠BCD+∠ACD=90°,即可求得结果。
(2)由(1)可知∠ABD=30°,根据已知易求得AD、AP、BP、BD的长度,再证明△APC∽△DPB、△CPB∽△APD得出它们的对应边成比例,再在Rt△ABC中,根据勾股定理,求出DP的长,将DP的长代入② ,就可以求出PC的长,继而求出CD。方法二、由①÷③得 A C : B C的值,根据AB=4求出BC的长,再由③和 ②,即可求出结果。
(3)要使弦CD最短,根据轴对称的相关知识,先找到点P的位置,即CD⊥AB于点P,连接OD,根据已知条件求出AP、OP的长,在Rt△POD中,运用锐角三角函数求出∠POD的度数,从而求出∠ACD,∠BCD的度数,即可求出m的值。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc>0;②b<a+c;③4ac﹣b2>0;④2a+b=0
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为给人们的生活带来方便,2017年兴化市准备在部分城区实施公共自行车免费服务.图1是公共自行车的实物图,图2是公共自行车的车架示意图,点A,D,C,E在同一条直线上,CD=35cm,DF=24cm,AF=30cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离(结果保留整数).
(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
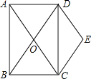
【题目】如图,矩形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 关于
关于![]() 的对称图形为
的对称图形为![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
①根据题意补全图形;
②若![]() =
=![]() ,请用等式表示线段
,请用等式表示线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设门市部专卖某产品,该每件成本每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
销售单位(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
日销售量 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设每天定的销价是不变的,且每天销售情况均服从这种规律.
(1)秋日销售量与销售价格之间满足的函数关系式;
(2)门市部原设定两名销售员,担当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b满足,![]() 且A(a,0)、B(0,b)
且A(a,0)、B(0,b)

(1) 如图,在x正半轴上有一点C(x,0).若△ABC的面积大于6,请直接写出x的取值范围____________;
(2)若在平面直角坐标系第四象限上存在一点N,N的坐标为(n,﹣n),满足4≤S△ABN≤8,求n的取值范围.
(3)若在平面直角坐标系上存在一点M,M的坐标为(m,﹣2m),请通过计算说明:无论m取何值△ABM的面积为定值,并求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为![]() .第一次操作:分别延长
.第一次操作:分别延长![]() ,
,![]() ,
,![]() 至点
至点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() ,顺次连接
,顺次连接![]() ,
,![]() ,
,![]() ,得到△
,得到△![]() .第二次操作:分别延长
.第二次操作:分别延长![]() ,
,![]() ,
,![]() 至点
至点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() ,顺次连接
,顺次连接![]() ,
,![]() ,
,![]() ,得到△
,得到△![]() ,…按此规律,要使得到的三角形的面积超过2020,最少经过多少次操作( )
,…按此规律,要使得到的三角形的面积超过2020,最少经过多少次操作( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
① 20.2×19.8 ;
②![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点P从点C开始,按
,若动点P从点C开始,按![]() 的路径运动,且速度为每秒1cm,设出发的时间为t秒.
的路径运动,且速度为每秒1cm,设出发的时间为t秒.

![]() 出发2秒后,求
出发2秒后,求![]() 的面积;
的面积;
![]() 当t为几秒时,BP平分
当t为几秒时,BP平分![]() ;
;
![]() 问t为何值时,
问t为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com