
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc>0;②b<a+c;③4ac﹣b2>0;④2a+b=0
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
【答案】A
【解析】解:①观察函数图象可知:a<0,c>0,﹣ ![]() >0,
>0,
∴b>0,
∴abc<0,①错误;②∵当x=﹣1时,y<0,
∴a﹣b+c<0,
∴b>a+c,②错误;③∵抛物线与x轴有两个交点,
∴△=b2﹣4ac>0,
∴4ac﹣b2<0,③错误;④∵抛物线的对称轴为直线x=﹣ ![]() =1,
=1,
∴b=﹣2a,
∴2a+b=0,④正确.
所以答案是:A.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,直线 AB与 x 轴,y 轴分别交于点 A和点 B,点 A的坐标为(1,0),且 2OA=OB.
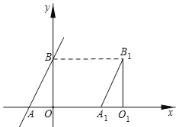
(1)求直线 AB 解析式;
(2)如图,将△A O B 向右平移 3 个单位长度,得到△A1O1B1,求线段 O B1的长;
(3)在(2)中△AOB 扫过的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
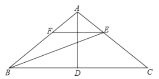
【题目】如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
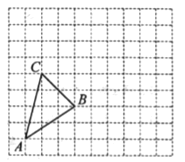
(1)画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(2)画出△ABC的中线AD;
(3)画出△ABC的高CE所在直线,标出垂足E:
(4)在(1)的条件下,线段AA1和CC1的关系是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场同时出售同样的水瓶和水杯,且定价相同,请根据图中提供的信息,回答下列问题:

(1)一个水瓶与一个水杯分别是多少元?(请列方程解应用题)
(2)为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和12个水杯,请问选择哪家商场购买更合算,并说明理由(水瓶和水杯必须在同一家购买).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中,AB为⊙O的直径,AB=4,P为AB上一点,过点P作⊙O的弦CD,设∠BCD=m∠ACD.
(1)已知 ![]() ,求m的值,及∠BCD、∠ACD的度数各是多少?
,求m的值,及∠BCD、∠ACD的度数各是多少?
(2)在(1)的条件下,且 ![]() ,求弦CD的长;
,求弦CD的长;
(3)当 ![]() 时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由.
时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com