
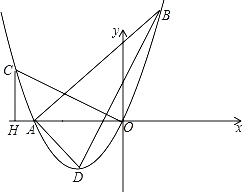
【题目】在平面直角坐标系xOy中,已知抛物线y=![]() x2+bx+c经过点A(﹣4,0)和B(2,6),其顶点为D.
x2+bx+c经过点A(﹣4,0)和B(2,6),其顶点为D.
(1)求此抛物线的表达式;
(2)求△ABD的面积;
(3)设C为该抛物线上一点,且位于第二象限,过点C作CH⊥x轴,垂足为点H,如果△OCH与△ABD相似,求点C的坐标.
【答案】(1)y=![]() x2+2x;(2)12;(3)点H的坐标为(﹣10,30)或(﹣
x2+2x;(2)12;(3)点H的坐标为(﹣10,30)或(﹣![]() ,
,![]() )
)
【解析】
(1)将点A、B的坐标代入抛物线表达式,即可求解;
(2)利用两点间的距离公式:得AB,AD,BD的值,从而得BD2=AB2+AD2,则△ABD为直角三角形,△ABD的面积=![]() AB×AD,即可求解;
AB×AD,即可求解;
(3)由△OCH与△ABD相似,得tan∠COH=tan∠ABD或tan∠ADB,即tan∠COH=![]() =
=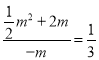 或3,进而即可求解.
或3,进而即可求解.
(1)将点A、B的坐标代入抛物线表达式得: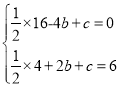 ,解得:
,解得:![]() ,
,
∴抛物线的表达式为:y=![]() x2+2x;
x2+2x;
(2)对于y=![]() x2+2x,顶点D(﹣2,﹣2),
x2+2x,顶点D(﹣2,﹣2),
∴AD=![]() ,
,
同理:AB=6![]() ,BD=4
,BD=4![]() ,
,
∴BD2=AB2+AD2,
∴△ABD为直角三角形,
∴△ABD的面积=![]() AB×AD=
AB×AD=![]() ×6
×6![]() ×2
×2![]() =12;
=12;
(3)在△ABD中,tan∠ABD=![]() ,
,
∵△OCH与△ABD相似,
∴tan∠COH=tan∠ABD或tan∠COH=tan∠ADB,
即:tan∠COH=![]() 或3,
或3,
设点C(m,![]() m2+2m),则tan∠COH=
m2+2m),则tan∠COH=![]() =
=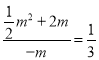 或3,
或3,
解得:m=﹣10或﹣![]() (不合题意的值已舍去),
(不合题意的值已舍去),
∴点H的坐标为(﹣10,30)或(﹣![]() ,
,![]() ).
).


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
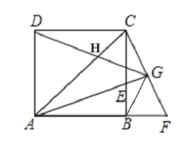
【题目】如图,ABCD为正方形,∠CAB的角平分线交BC于点E,过点C作CF⊥AE交AE的延长线于点G,CF与AB的延长线交于点F,连接BG、DG、与AC相交于点H,则下列结论:①![]() ABE
ABE![]()
![]() CBF;②GF=CG;③BG⊥DG;④
CBF;②GF=CG;③BG⊥DG;④![]() ,其中正确的是______.
,其中正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
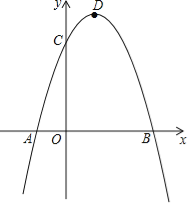
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的重心为G,△DEF与△ABC关于点G成中心对称,将它们重叠部分的面积记作S1,△ABC的面积记作S2,那么![]() 的值是_____
的值是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性;
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每一幅图中均含有若干个正方形,第①个图形中含有1个正方形,第②个图形中含有5个正方形,按此规律下去,则第⑥个图形含有正方形的个数是( )
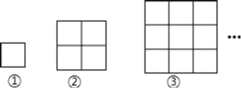
A.102B.91C.55D.31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.

(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作菱形ABMN与菱形BCEF,点F在BM边上,AB=n,∠ABM=60°,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn,当n≥2时,Sn﹣Sn﹣1=__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com