Question

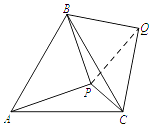
【题目】如图，P是等边△ABC内的一点，且PA=5，PB=4，PC=3，将△APB绕点B逆时针旋转，得到△CQB．求：

（1）点P与点Q之间的距离；
（2）求∠BPC的度数．

Answer 1

【答案】
（1）解：连结PQ，如图，

∵△ABC是等边三角形

∴∠ABC=60°，BA=BC，

∵△QCB是△PAB绕点B逆时针旋转得到的，

∴BP=BQ，∠PBQ=∠ABC=60°，CQ=AP=5，

∵BP=BQ=4，∠PBQ=60°，

∴△PBQ是等边三角形，

∴PQ=PB=4

（2）解：∵QC=5，PC=3，PQ=4，

而32+42=52，

∴PC2+PQ2=CQ2，

∴△PCQ是直角三角形，且∠QPC=90°，

∵△PBQ是等边三角形，

∴∠BPQ=60°，

∴∠BPC=∠BPQ+∠QPC=60°+90°=150°．

【解析】（1）连结PQ，如图，根据等边三角形得性质得∠ABC=60°，BA=BC，再利用旋转的性质得BP=BQ，∠PBQ=∠ABC=60°，CQ=AP=5，BP=BQ=4，∠PBQ=60°，于是可判断△PBQ是等边三角形，所以PQ=PB=4；（2）先利用勾股定理的逆定理证明△PCQ是直角三角形，且∠QPC=90°，再加上∠BPQ=60°，然后计算∠BPQ+∠QPC即可．
【考点精析】认真审题，首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)，还要掌握旋转的性质(①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了)的相关知识才是答题的关键．