
【题目】综合与实践
问题情境
在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,且交直线
,且交直线![]() 于点
于点![]() .
.



(1)如图1,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.
自主探究
(2)如图2,当点![]() 在线段
在线段![]() 上时,其它条件不变,请猜想
上时,其它条件不变,请猜想![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
拓展延伸
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)证明见解析;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() .
.
【解析】
(1)根据等腰直角三角形的性质得到∠A=∠ABC,根据同角的余角相等得到∠CBG=∠ACE,根据ASA公理证明△ACE≌△CBG;
(2)同理即可证明△ACE≌△CBG;
(3)CG=AE.
解:(1)在Rt△ABC中,
∵AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
在△ACE和△CBG中,
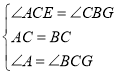 ,
,
∴△ACE≌△CBG;
(2)结论仍然成立,即△ACE≌△CBG.
理由如下:在Rt△ABC中,
∵AC=BC,
∴∠A=∠ABC=45°.
∵点D是AB的中点,
∴∠BCG=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠BCG.
∵BF⊥CE,
∴∠CBG+∠BCF=90°.
∵∠ACE+∠BCF=90°,
∴∠CBG=∠ACE,
∴△ACE≌△CBG;
(3)CG=AE.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )

A. ![]() 米 B. 2米 C. 2
米 B. 2米 C. 2![]() 米 D. 3米
米 D. 3米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )

A. ac>0 B. 当x>0时,y随x的增大而减小
C. 2a﹣b=0 D. 方程ax2+bx+c=0的两根是x1=﹣1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,点![]() 是边
是边![]() 上一点,且∠ACD=∠AOB.
上一点,且∠ACD=∠AOB.
(1)尺规作图:作∠AOB的平分线OE,交CD于点E.(保留作图痕迹,不写作法)
(2)在(1)所作图形中,若∠AOB=30°,OC=4,求△OCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(分钟)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:
(1)从消毒开始,经多长时间,教室内每立方米空气含药量为4mg.
(2)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是一面长
是一面长![]() 米的墙,用总长为
米的墙,用总长为![]() 米的木栅栏(图中的虚线)围一个矩形场地
米的木栅栏(图中的虚线)围一个矩形场地![]() ,中间用栅栏隔成同样三块.若要围成的矩形面积为
,中间用栅栏隔成同样三块.若要围成的矩形面积为![]() 平方米,则
平方米,则![]() 的长为________米.
的长为________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店四月份购进甲、乙两种文具共80件,分别用去400元、1200元,甲种文具每件的进价是乙种文具的![]() .请解答下列问题:
.请解答下列问题:
(1)求甲、乙两种文具每件的进价;
(2)五月份文具店决定再次购进甲、乙两种文具共80件,进价不变,甲、乙文具每件售价分别是15元、40元.若80件文具全部售出,求销售甲乙文具获利y(元)与购进甲种文具x(件)之间的函数解析式;
(3)在(2)的条件下,销售前文具店决定从这80件文具中拿出一部分,赠送给某校在“牡丹江首届汉字听写电视大赛”获一、二等奖的6名同学,作为奖品,其余文具全部售出.已知一等奖每人1件甲种文具,3件乙种文具;二等奖每人4件甲种文具,1件乙种文具,这些奖品总进价超过450元,文具店购进的80件文具仅获利30元.请直接写出文具店购进甲、乙两种文具的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com