
【题目】如图,已知∠AOB,点![]() 是边
是边![]() 上一点,且∠ACD=∠AOB.
上一点,且∠ACD=∠AOB.
(1)尺规作图:作∠AOB的平分线OE,交CD于点E.(保留作图痕迹,不写作法)
(2)在(1)所作图形中,若∠AOB=30°,OC=4,求△OCE的面积.

科目:初中数学 来源: 题型:
【题目】一个长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板点A位置的变化为A→Al→A2,其中第二次翻滚被面上一小木块挡住,使木板与桌面成30°的角,则点A滚到A2位置时共走过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1是一个重要公式的几何解释.请你写出这个公式: ;
(2)如图2,已知![]() ,
,![]() ,且
,且![]() 三点共线.
三点共线.
试证明![]() ;
;

(3)勾股定理是几何学中的明珠,千百年来,人们对它的证明趋之若骛,有资料表明,关于勾股定理的证明方法已有500余种.课本中介绍了比较有代表性的赵爽弦图.
伽菲尔德(Garfield,1881年任美国第20届总统)利用图2证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),请你写出该证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
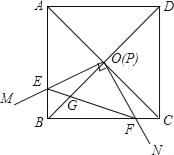
【题目】如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是_____.
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(4)OGBD=AE2+CF2.
;(4)OGBD=AE2+CF2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,且交直线
,且交直线![]() 于点
于点![]() .
.



(1)如图1,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.
自主探究
(2)如图2,当点![]() 在线段
在线段![]() 上时,其它条件不变,请猜想
上时,其它条件不变,请猜想![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
拓展延伸
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在ΔABC中,AB=AC,周长为24,AC边上的中线BD把ΔABC分成周长为9和15的两个部分,则ΔABC各边的长分别为( )
A.10、10、4B.6、6、12C.5、9、10D.10、10、4或6、6、12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com