
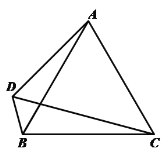
【题目】如图,在等边△![]() 中,作
中,作![]() ,边CD、BD交于点D,连接AD.
,边CD、BD交于点D,连接AD.
(1)请直接写出![]() 的度数;
的度数;
(2)求![]() 的度数;
的度数;
(3)用等式表示线段AC、BD、CD三者之间的数量关系,并证明.
【答案】(1)60°;(2)![]() ;(3)
;(3)![]() .证明见解析.
.证明见解析.
【解析】
(1)设AB与CD的交点为O,有![]() ,
,![]() ,根据三角形内角和定理可得:
,根据三角形内角和定理可得:![]() =
=![]() =60°;
=60°;
(2)有两角相等得△AOC∽△DOB,所以![]() ,且夹角相等,再得△AOD∽△COB,从而求得
,且夹角相等,再得△AOD∽△COB,从而求得![]() .
.
(3)现由SAS证明△ADE≌△ADB,再证明![]() 是等腰直角三角形即可解答.
是等腰直角三角形即可解答.
(1)![]() ;
;
(2)设AB与CD的交点为O.
∵![]() ,
,![]() ,
,
∴△AOC∽△DOB.
∴![]() .
.
∵![]() ,
,
∴△AOD∽△COB.
∴![]() .
.
(3)答案一:线段AC、BD、CD三者之间的数量关系为![]() .
.
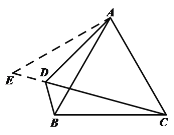
证明:如图,延长CD到点E,使![]() ,连接AE.
,连接AE.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在△ADE和△ADB中,

∴△ADE≌△ADB.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
另一种证法:延长BD到点E,使![]() ,连接AE.
,连接AE.
答案二:线段AC、BD、CD三者之间的数量关系为![]() .
.
证明:如图,在D C上截取![]() ,连接BE,过点A作AF⊥CD于点F.
,连接BE,过点A作AF⊥CD于点F.

可证△ADB≌△CEB,可得![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1).若以C,D,E(E在格点上)为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
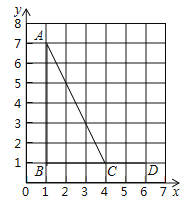
A. (6,0) B. (4,2) C. (6,5) D. (6,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形![]() (三角形的三个顶点都在小正方形的顶点上)
(三角形的三个顶点都在小正方形的顶点上)
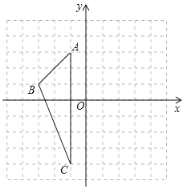
(1)写出![]() 的面积;
的面积;
(2)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)写出点![]() 及其对称点
及其对称点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
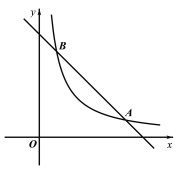
【题目】如图,在平面直角坐标系xOy中,直线![]() 与函数
与函数![]() 的图象的两个交点分别为A(a,1)、B.
的图象的两个交点分别为A(a,1)、B.
(1)求![]() ,a的值及点B的坐标;
,a的值及点B的坐标;
(2)过点P(n,0)作x轴的垂线,与直线![]() 和函数
和函数![]() 的图象分别交于点M,N,当点M在点N上方时,写出n的取值范围.
的图象分别交于点M,N,当点M在点N上方时,写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,已知AB>BC.
(1)实践与操作:作∠ADC的平分线交AB于点E,在DC上截取DF=AD,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形AEFD的形状,并给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已知点![]() 的坐标(-1,4),点
的坐标(-1,4),点![]() 的位置如图所示
的位置如图所示
(1)写出图中点![]() 的坐标: ________;
的坐标: ________;
(2)求![]() 的面积;
的面积;
(3)画出![]() 关于
关于![]() 轴的对称图形,点
轴的对称图形,点![]() 的对称点分别为
的对称点分别为![]() ,写出
,写出![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
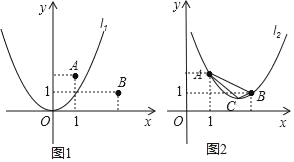
【题目】如图1,在平面直角坐标系中,点A的坐标为(1,2),点B的坐标为(3,1),二次函数y=x2的图象记为抛物线l1.
(1)平移抛物线l1,使平移后的抛物线经过点A,但不经过点B.请写出平移后抛物线的解析式(任写一个即可);
(2)平移抛物线l1,使平移后的抛物线经过A,B两点,记为抛物线l2,求抛物线l2的函数关系式;
(3)如图2,设抛物线l2的顶点为C,K为y轴上一点.若S△ABK=S△ABC,求点K的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com