
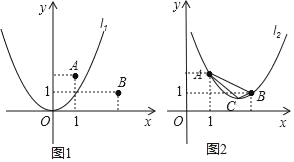
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЌЖўДЮКЏЪ§y=x2ЕФЭМЯѓМЧЮЊХзЮяЯпl1ЃЎ
ЃЈ1ЃЉЦНвЦХзЮяЯпl1ЃЌЪЙЦНвЦКѓЕФХзЮяЯпОЙ§ЕуAЃЌЕЋВЛОЙ§ЕуBЃЎЧыаДГіЦНвЦКѓХзЮяЯпЕФНтЮіЪНЃЈШЮаДвЛИіМДПЩЃЉЃЛ
ЃЈ2ЃЉЦНвЦХзЮяЯпl1ЃЌЪЙЦНвЦКѓЕФХзЮяЯпОЙ§AЃЌBСНЕуЃЌМЧЮЊХзЮяЯпl2ЃЌЧѓХзЮяЯпl2ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЩшХзЮяЯпl2ЕФЖЅЕуЮЊCЃЌKЮЊyжсЩЯвЛЕуЃЎШєSЁїABK=SЁїABCЃЌЧѓЕуKЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=x2+1ЃЈ2ЃЉЃЈ0ЃЌ![]() ЃЉЛђЃЈ0ЃЌ
ЃЉЛђЃЈ0ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉПЩНЋХзЮяЯпb1ЯђЩЯЦНвЦЃЌЩшЦНвЦКѓЕФХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃКy=x2+bЃЌгЩЕуAЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉИљОнЬтвтПЩЩшХзЮяЯпb2ЕФКЏЪ§ЙиЯЕЪНЮЊy=x2+bx+cЃЌгЩЕуAЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉЪзЯШИљОнЬтвтЧѓЕУЕуCЕФзјБъЃЌМДПЩЧѓЕУЁїABCЕФУцЛ§ЃЌШЛКѓЗжБ№ДгЕуKдкAЕФЩЯЗНгыЯТЗНШЅЗжЮіЧѓНтЃЌМДПЩЧѓЕУЕуKЕФзјБъЃЎ
НтЃКЃЈ1ЃЉЯђЩЯЦНвЦХзЮяЯпb1ЃЌЪЙЦНвЦКѓЕФХзЮяЯпОЙ§ЕуAЃЌ
ЩшЦНвЦКѓЕФХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃКy=x2+bЃЌ
ЁпЕуAЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌ
Ёр2=1+bЃЌ
НтЕУЃКb=1ЃЌ
ЁрЦНвЦКѓЕФХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃКy=x2+1ЃЛ
ЁпЕуBЕФзјБъЮЊЃЈ3ЃЌ1ЃЉЃЌ
Ёр32+1Ёй1ЃЌ
ЁрЦНвЦКѓЕФХзЮяЯпЕФКЏЪ§ЙиЯЕЪНЃКy=x2+1ЃЛ
ЙЪД№АИЮЊЃКy=x2+1ЃЎ
ЃЈ2ЃЉЩшЁпХзЮяЯпb2ОЙ§AЃЌBСНЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК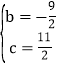 ЃЌ
ЃЌ
ЁрХзЮяЯпb2ЕФКЏЪ§ЙиЯЕЪНЮЊЃКy=x2Љ![]() x+
x+![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЁпy=x2Љ![]() x+
x+![]() =ЃЈxЉ
=ЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Й§ЕуCзїCGЁЭyжсЃЌBFЁЭyжсЃЌAEЁЭyжсЃЌ
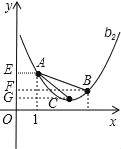
ЁрAE=1ЃЌBF=3ЃЌCG=![]() ЃЌEF=2Љ1=1ЃЌFG=1Љ
ЃЌEF=2Љ1=1ЃЌFG=1Љ![]() =
=![]() ЃЌEG=2Љ
ЃЌEG=2Љ![]() =
=![]() ЃЌ
ЃЌ
ЁрSЁїABC=SЬнаЮABFE+SЬнаЮBCGFЉSЬнаЮACGE=![]() ЃЈAE+BFЃЉEF+
ЃЈAE+BFЃЉEF+![]() ЃЈCG+BFЃЉGFЉ
ЃЈCG+BFЃЉGFЉ![]() ЃЈAE+CGЃЉEG=
ЃЈAE+CGЃЉEG=![]() ЃЌ
ЃЌ
ШєKдкAЕуЩЯЗНЃЌзјБъЮЊЃЈ0ЃЌyЃЉ
SЁїABK=SЁїBNKЉSЁїAMKЉSЬнаЮABNM=![]() BNNKЉ
BNNKЉ![]() AMMKЉ
AMMKЉ![]() ЃЈAM+BNЃЉMN=
ЃЈAM+BNЃЉMN=![]() ЁС3ЁСЃЈyЉ1ЃЉЉ
ЁС3ЁСЃЈyЉ1ЃЉЉ![]() ЁС1ЁСЃЈyЉ2ЃЉЉ
ЁС1ЁСЃЈyЉ2ЃЉЉ![]() ЁСЃЈ1+3ЃЉЁС1=
ЁСЃЈ1+3ЃЉЁС1=![]() ЃЌ
ЃЌ
ЁпSЁїABK=SЁїABCЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
НтЕУЃКy=![]() ЃЌ
ЃЌ
дђЕуKЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЭЌРэЃКШєKдкAЕФЯТЗНЪБЃЌдђЕуKЃЈ0ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЁрЕуKЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЛђЃЈ0ЃЌ
ЃЉЛђЃЈ0ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ


 ПЮЬУШЋНтзжДЪОфЖЮЦЊеТЯЕСаД№АИ
ПЮЬУШЋНтзжДЪОфЖЮЦЊеТЯЕСаД№АИ ВНВНИпПкЫуЬтПЈЯЕСаД№АИ
ВНВНИпПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
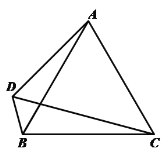
ЁОЬтФПЁПШчЭМЃЌдкЕШБпЁї![]() жаЃЌзї
жаЃЌзї![]() ЃЌБпCDЁЂBDНЛгкЕуDЃЌСЌНгAD.
ЃЌБпCDЁЂBDНЛгкЕуDЃЌСЌНгAD.
ЃЈ1ЃЉЧыжБНгаДГі![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ3ЃЉгУЕШЪНБэЪОЯпЖЮACЁЂBDЁЂCDШ§епжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіВЛЭИУїЕФДќжазАга5ИіЛЦЧђЁЂ13ИіКкЧђКЭ22ИіКьЧђЃЌЫќУЧГ§беЩЋЭтЖМЯрЭЌЁЃ
ЃЈ1ЃЉЧѓДгДќжаУўГівЛИіЧђЪЧЛЦЧђЕФИХТЪЃЛ
ЃЈ2ЃЉЯжДгДќжаШЁГіШєИЩИіКкЧђЃЌВЂЗХШыЯрЭЌЪ§СПЕФЛЦЧђЃЌНСАшОљдШКѓЃЌЪЙДгДќжаУўГівЛИіЧђЪЧЛЦЧђЕФИХТЪВЛаЁгк![]() ЃЌЮЪжСЩйШЁГіСЫЖрЩйИіКкЧђЃП
ЃЌЮЪжСЩйШЁГіСЫЖрЩйИіКкЧђЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯёдкЕквЛЯѓЯогавЛИіЙЋЙВЕуЃЌЦфКсзјБъЮЊ1ЃЌдђвЛДЮКЏЪ§
ЕФЭМЯёдкЕквЛЯѓЯогавЛИіЙЋЙВЕуЃЌЦфКсзјБъЮЊ1ЃЌдђвЛДЮКЏЪ§![]() ЕФЭМЯёПЩФмЪЧЃЈ ЃЉ
ЕФЭМЯёПЩФмЪЧЃЈ ЃЉ
A. 
B. 
C. 
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
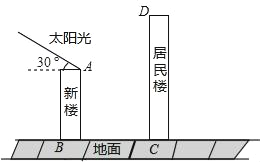
ЁОЬтФПЁПФГзЁеЌаЁЧјгавЛЖАУцГЏе§ФЯЕФОгУёТЅЃЈШчЭМЃЉЃЌИУОгУёТЅЕФвЛТЅИпЮЊ6УзЕФаЁЧјГЌЪаЃЌГЌЪавдЩЯЪЧОгУёзЁЗПЃЎдкИУТЅЕФЧАУц15УзДІвЊИЧвЛЖАИп20УзЕФаТТЅЃЎвбжЊЖЌМОе§ЮчЕФбєЙтгыЫЎЦНЯпЕФМаНЧЮЊ30ЁуЪБЃЎ
ЃЈ1ЃЉаТТЅЕФНЈдьЖдГЌЪавдЩЯЕФОгУёзЁЗПЖЌМОе§ЮчЕФВЩЙтЪЧЗёгагАЯьЃЌЮЊЪВУДЃП
ЃЈ2ЃЉШєвЊЪЙГЌЪаЖЌМОе§ЮчЕФВЩЙтВЛЪмгАЯьЃЌаТТЅгІНЈдкЯрОрОгУёТЅжСЩйЖрЩйУзЕФЕиЗНЃЌЮЊЪВУДЃПЃЈНсЙћБЃСєећЪ§ЃЌВЮПМЪ§ОнЃКsin30ЁуЁж0.5ЃЌcos30ЁуЁж0.87ЃЌtan30ЁуЁж0.58ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,КЏЪ§![]() КЭ
КЭ![]() (
(![]() ЪЧГЃЪ§,Чв
ЪЧГЃЪ§,Чв![]() )дкЭЌвЛЦНУцжБНЧзјБъЯЕЕФЭМЯѓПЩФмЪЧЃЈ ЃЉ
)дкЭЌвЛЦНУцжБНЧзјБъЯЕЕФЭМЯѓПЩФмЪЧЃЈ ЃЉ
A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
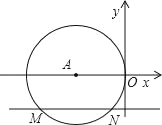
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁбAгыyжсЯрЧагкдЕуOЃЌЦНаагкxжсЕФжБЯпНЛЁбAгкMЁЂNСНЕуЃЌШєЕуMЕФзјБъЪЧЃЈЉ4ЃЌЉ2ЃЉЃЌдђЯвMNЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() НЧаЮгыСНзјБъжсЗжБ№НЛгк
НЧаЮгыСНзјБъжсЗжБ№НЛгк![]() ЃЌжБЯп
ЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() гыжБЯп
гыжБЯп![]() НЛгкЕу
НЛгкЕу![]()
![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕ
ЕФжЕ
ЃЈ2ЃЉжБНгаДГіВЛЕШЪН![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉЕу![]() дк
дк![]() ЩЯЃЌШчЙћ
ЩЯЃЌШчЙћ![]() ЕФУцЛ§ЮЊ4ЃЌЕу
ЕФУцЛ§ЮЊ4ЃЌЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
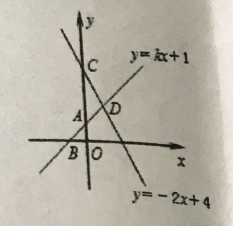
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌЕуEЃЌFЗжБ№дкБпABЃЌBCЩЯЃЌЧвAE=![]() ABЃЌНЋОиаЮбижБЯпEFелЕўЃЌЕуBЧЁКУТфдкADБпЩЯЕФЕуPДІЃЌСЌНгBPНЛEFгкЕуQЃЌЖдгкЯТСаНсТлЃКЂйEF=2BEЃЛЂкPF=2PEЃЛЂлFQ=4EQЃЛЂмЁїPBFЪЧЕШБпШ§НЧаЮЃЎЦфжае§ШЗЕФЪЧЃЈ ЃЉ
ABЃЌНЋОиаЮбижБЯпEFелЕўЃЌЕуBЧЁКУТфдкADБпЩЯЕФЕуPДІЃЌСЌНгBPНЛEFгкЕуQЃЌЖдгкЯТСаНсТлЃКЂйEF=2BEЃЛЂкPF=2PEЃЛЂлFQ=4EQЃЛЂмЁїPBFЪЧЕШБпШ§НЧаЮЃЎЦфжае§ШЗЕФЪЧЃЈ ЃЉ

A. ЂйЂк B. ЂкЂл C. ЂйЂл D. ЂйЂм
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com