练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

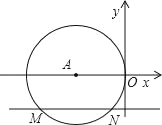
    【题目】如图，在平面直角坐标系中，⊙A与y轴相切于原点O，平行于x轴的直线交⊙A于M、N两点，若点M的坐标是（﹣4，﹣2），则弦MN的长为_____．

    【答案】3

    【解析】

    可先设半径的大小，由此得出A点的方程．连接AM、AN根据等腰三角形的性质即可得出AN的长度，再根据两点之间的距离公式即可解出N点的坐标，从而求得MN的长度．

    分别过点M、N作x轴的垂线，过点A作AB⊥MN，连接AN

    设⊙A的半径为r．
    则AN=OA=r，AB=2，
    ∵AB⊥MN，
    ∴BM=BN，
    ∴BN=4-r；
    则在Rt△ABN中，根据勾股定理，
    得AB2+BN2=AN2，即：22+（4-r）2=r2，解得r=2.5，
    则N到y轴的距离为1，
    又∵点N在第三象限，
    ∴N的坐标为（-1，-2）；
    ∴MN=3；
    故答案是：3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在直角坐标平面内，已知点的坐标(-1，4)，点的位置如图所示

    （1）写出图中点的坐标： ________；

    （2）求的面积；

    （3）画出关于轴的对称图形，点的对称点分别为，写出的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲乙两人同时同地沿同一路线开始攀登一座600米高的山，甲的攀登速度是乙的1.2倍，他比乙早20分钟到达顶峰.甲乙两人的攀登速度各是多少？如果山高为米，甲的攀登速度是乙的倍，并比乙早分钟到达顶峰，则两人的攀登速度各是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

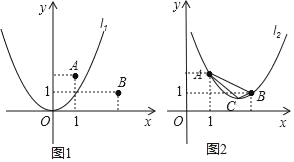
    【题目】如图1，在平面直角坐标系中，点A的坐标为（1，2），点B的坐标为（3，1），二次函数y=x2的图象记为抛物线l1．

    （1）平移抛物线l1，使平移后的抛物线经过点A，但不经过点B．请写出平移后抛物线的解析式（任写一个即可）；

    （2）平移抛物线l1，使平移后的抛物线经过A，B两点，记为抛物线l2，求抛物线l2的函数关系式；

    （3）如图2，设抛物线l2的顶点为C，K为y轴上一点．若S△ABK=S△ABC，求点K的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

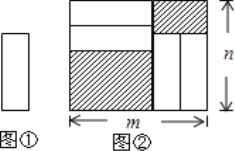
    【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m，宽为n)的盒子底部(如图②)，盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

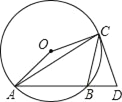
    【题目】如图，点A、B、C均在⊙O上，过点C作⊙O的切线交AB的延长线于点D，∠ACB=45°，∠AOC=150°．

    （1）求证：CD=CB；

    （2）⊙O的半径为，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABP与是两个全等的等边三角形，且，有下列四个结论：①，②，③，④四边形ABCD是轴对称图形，其中正确的有

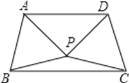
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在一笔直的海岸线l上有AB两个观测站，A在B的正东方向，AB=2（单位：km）．有一艘小船在点P处，从A测得小船在北偏西60°的方向，从B测得小船在北偏东45°的方向．（结果都保留根号）

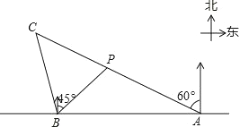
    （1）求点P到海岸线l的距离；

    （2）小船从点P处沿射线AP的方向航行一段时间后，到点C处，此时，从B测得小船在北偏西15°的方向．求点C与点B之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】1876年，美国总统Garfield用如图所示的两个全等的直角三角形证明了勾股定理，若图中，，，则下面结论错误的是( )

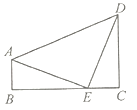
    A. B. C. D. 是等腰直角三角形

    查看答案和解析>>

    同步练习册答案