
【题目】如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)
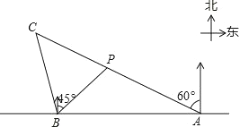
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.
【答案】(1)点P到海岸线l的距离为(![]() ﹣1)km;(2)点C与点B之间的距离为
﹣1)km;(2)点C与点B之间的距离为![]() km.
km.
【解析】试题分析:(1)过点P作PD⊥AB于点D,设PD=xkm,先解Rt△PBD,用含x的代数式表示BD,再解Rt△PAD,用含x的代数式表示AD,然后根据BD+AD=AB,列出关于x的方程,解方程即可;(2)过点B作BF⊥AC于点F,先解Rt△ABF,得出BF=![]() AB=1km,再解Rt△BCF,得出BC=
AB=1km,再解Rt△BCF,得出BC=![]() BF=
BF=![]() km.
km.
试题解析:(1)如图,过点P作PD⊥AB于点D.设PD=xkm.
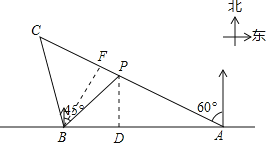
在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°,
∴BD=PD=xkm.
在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°,
∴AD=![]() PD=
PD=![]() xkm.
xkm.
∵BD+AD=AB,
∴x+![]() x=2,x=
x=2,x=![]() ﹣1,
﹣1,
∴点P到海岸线l的距离为(![]() ﹣1)km;
﹣1)km;
(2)如图,过点B作BF⊥AC于点F.根据题意得:∠ABC=105°,
在Rt△ABF中,∠AFB=90°,∠BAF=30°,
∴BF=![]() AB=1km.
AB=1km.
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC=45°.
在Rt△BCF中,∠BFC=90°,∠C=45°,
∴BC=![]() BF=
BF=![]() km,
km,
∴点C与点B之间的距离为![]() km.
km.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球、13个黑球和22个红球,它们除颜色外都相同。
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后,使从袋中摸出一个球是黄球的概率不小于![]() ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣4,﹣2),则弦MN的长为_____.
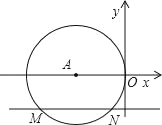
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 角形与两坐标轴分别交于
角形与两坐标轴分别交于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与直线
与直线![]() 交于点
交于点![]()
![]() 面积为
面积为![]() .
.
(1)求![]() 的值
的值
(2)直接写出不等式![]() 的解集;
的解集;
(3)点![]() 在
在![]() 上,如果
上,如果![]() 的面积为4,点
的面积为4,点![]() 的坐标.
的坐标.
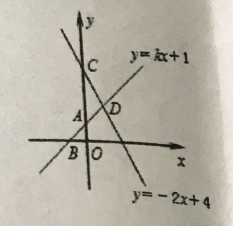
查看答案和解析>>
科目:初中数学 来源: 题型:
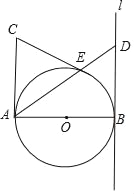
【题目】如图,AB=AC=8,∠BAC=90,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连结DA交⊙O点E.
(1)当点D在AB上方且BD=6时,求AE的长;
(2)当CE恰好与⊙O相切时,求BD的长为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】崂山区某班全体同学参加了为一名因工受伤女教师捐款的活动,该班同学捐款情况的部分统计图如图所示:
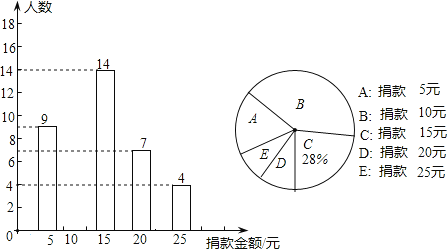
(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款金额的众数;
(3)该班平均每人捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扶梯AB的坡比(BE与AE长度之比)为4:3,滑梯CD的坡比(CF与DF长度之比)为1:2,设AE=30米,BC=30米,一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,他共经过了多少路程(即AB+BC+CD的长度)?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )

A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“知识改变命运,科技繁荣祖国.”为提升中小学生的科技素养,我区每年都要举办中小学科技节.为迎接比赛,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节项目的比赛,每人进行了4次测试,对照一定的标准,得分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,你打算安排谁代表学校参赛?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com