
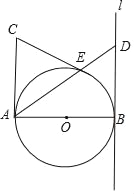
【题目】如图,AB=AC=8,∠BAC=90,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连结DA交⊙O点E.
(1)当点D在AB上方且BD=6时,求AE的长;
(2)当CE恰好与⊙O相切时,求BD的长为多少?
【答案】(1)AE=![]() ;(2)BD= 4.
;(2)BD= 4.
【解析】
(1)连接BE,在Rt△ABD中,利用勾股定理求出AD的长,进而利用直角三角形等面积求出BE的长,在Rt△ABE中,利用勾股定理即可求出AE的长。
(2)连接OC,证明△ABD≌△CAO,根据全等三角形的性质即可求出BD的长.
解:(1)∵AB为直径,
∴∠AEB=90°,
∵BD为切线,
∴AB⊥BD,
∴∠ABD=90°,
在Rt△ABD中, ![]()
∵![]()
∴![]()
在Rt△ABE中, ![]()
(2)连接OC,如图,
∵∠BAC=90°,
∴CA为⊙O的切线,
∵CE为⊙O的切线,
∴CA=CE,
而OA=OE,
∴OC垂直平分AE,
∴∠1+∠3=90°,
而∠1+∠2=90°,
∴∠2=∠3,
而AB=CA,∠CAO=∠ABD,
∴△ABD≌△CAO,
∴BD=AO=4.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠,使点D与点B重合,点C落在点C′的位置上.
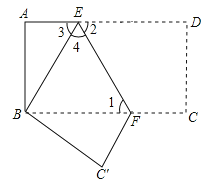
⑴若∠1=50°,求∠2、∠3的度数;
⑵若AB=7,DE=8,求CF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
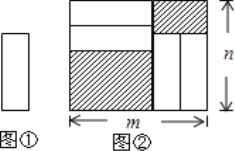
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
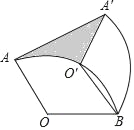
【题目】如图,将半径为6,圆心角为120°的扇形OAB绕点B顺时针旋转60°,点O,A的对应点分别为O′,A′,连接AA′,在图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.(结果都保留根号)
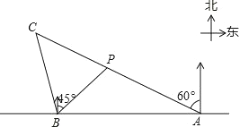
(1)求点P到海岸线l的距离;
(2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.

(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 ;
(2)抽查C厂家的合格零件为 件,并将图1补充完整;
(3)通过计算说明合格率排在前两名的是哪两个厂家.
查看答案和解析>>
科目:初中数学 来源: 题型:
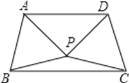
【题目】已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b, 请写出求tan∠ADB的思路.(不用写出计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
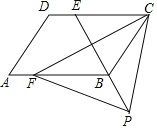
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com