
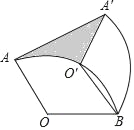
【题目】如图,将半径为6,圆心角为120°的扇形OAB绕点B顺时针旋转60°,点O,A的对应点分别为O′,A′,连接AA′,在图中阴影部分的面积是_____.
【答案】18![]() ﹣6π.
﹣6π.
【解析】
连接OO′,根据旋转的性质得到∠OBO′=60°,推出△OBO′是等边三角形,得到∠BOO′=60°,推出△OO′B是等边三角形,得到∠AO′B=120°,得到∠O′A′B=∠O′BA′=30°,根据图形的面积公式即可得到答案.
连接OO′,
∵将半径为6,圆心角为120°的扇形OAB绕点B顺时针旋转60°,
∴∠OBO′=60°,
∴△OAO′是等边三角形,
∴∠AOO′=60°,OO′=OA,
∴当O′中⊙O上,
∵∠AOB=120°,
∴∠O′OB=60°,
∴△OO′B是等边三角形,
∴∠AO′B=120°,
∵∠AO′A′=120°,
∴∠A′O′B=120°,
∴∠O′A′B=∠O′BA′=30°,
∴图中阴影部分的面积=S△A′O′B-(S扇形O′OB-S△OO′B)=![]() 18
18![]() ﹣6π.
﹣6π.
故答案是:18![]() ﹣6π.
﹣6π.


科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为8cm,点P从点C出发,以1cm/秒的速度由C向B匀速运动,点Q从点C出发,以2cm/秒的速度由C向A匀速运动,AP、BQ交于点M,当点Q到达A点时,P、Q两点停止运动,设P、Q两点运动的时间为t秒,若∠AMQ=60°时,则t的值是( )
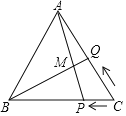
A.1B.2C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G.
(1)猜想BG与EG的数量关系.并说明理由;
(2)延长DE,BA交于点H,其他条件不变,
①如图2,若∠ADC=60°,求![]() 的值;
的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出![]() 的值.(用含α的三角函数表示)
的值.(用含α的三角函数表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
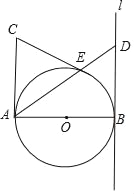
【题目】如图,AB=AC=8,∠BAC=90,直线l与以AB为直径的⊙O相切于点B,点D是直线l上任意一动点,连结DA交⊙O点E.
(1)当点D在AB上方且BD=6时,求AE的长;
(2)当CE恰好与⊙O相切时,求BD的长为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=50cm,BC=30cm,AC=40cm.
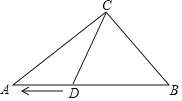
(1)求证:∠ACB=90°
(2)求AB边上的高.
(3)点D从点B出发在线段AB上以2cm/s的速度向终点A运动,设点D的运动时间为t(s).
①BD的长用含t的代数式表示为 .
②当△BCD为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com