
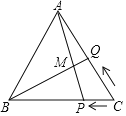
【题目】如图,等边△ABC的边长为8cm,点P从点C出发,以1cm/秒的速度由C向B匀速运动,点Q从点C出发,以2cm/秒的速度由C向A匀速运动,AP、BQ交于点M,当点Q到达A点时,P、Q两点停止运动,设P、Q两点运动的时间为t秒,若∠AMQ=60°时,则t的值是( )
A.1B.2C.![]() D.3
D.3
【答案】C
【解析】
由等边三角形性质可得:AC=BC=AB=8cm,∠BAC=∠ABC=∠C=60°,根据题意可得:CP=tcm,CQ=2tcm,进而可得:BP=(8-t)cm,AQ=(8-2t)cm,根据三角形外角性质可得:∠ABQ=∠CAP,即可证明:△ABQ≌△CAP(ASA),即可求得t的值.
∵△ABC是等边三角形
∴AC=BC=AB=8cm,∠BAC=∠ABC=∠C=60°
由题意,得:CP=tcm,CQ=2tcm,
∴BP=(8-t)cm,AQ=(8-2t)cm,
∵∠ABQ+∠BAP=∠AMQ=60°,∠CAP+∠BAP=∠BAC=60°
∴∠ABQ=∠CAP
在△ABQ和△CAP中

∴△ABQ≌△CAP(ASA)
∴AQ=CP
∴8-2t=t,解得:t=![]() (秒)
(秒)
故选:C.



科目:初中数学 来源: 题型:
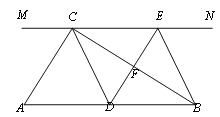
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时.
①求证:四边形BECD是菱形;
②当∠A为多少度时,四边形BECD是正方形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校允许学生在同个系列的校服里选择不同款式,新生入学后,学校就新生对校服款式选择情况作了抽样调查,调查分为款式A、B、C、D四种,每位新生只能选择一种款式,现将调查统计结果制成了如下两幅不完整的统计图,请结合这两幅统计图,回答下列问题:
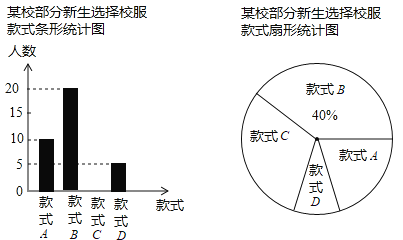
(1)在本次调查中,一共抽取了多少名新生,并补全条形统计图;
(2)若该校有847名新生,服装厂已生产了270套B款式的校服,请你按相关统计知识判断是否还要继续生产B款式的校服?
查看答案和解析>>
科目:初中数学 来源: 题型:
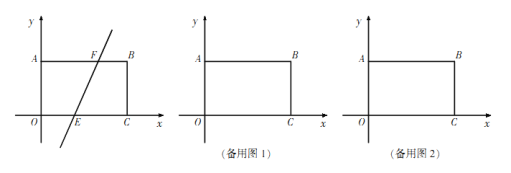
【题目】在平面直角坐标系中,长方形![]() 的边
的边![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 的坐标是(5,3),直线
的坐标是(5,3),直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() .
.
(1)用含![]() 的代数式表示点
的代数式表示点![]() 的坐标;
的坐标;
(2)若![]() ,当
,当![]() 为何值时,
为何值时, ![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠,使点D与点B重合,点C落在点C′的位置上.
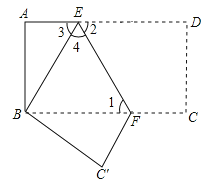
⑴若∠1=50°,求∠2、∠3的度数;
⑵若AB=7,DE=8,求CF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
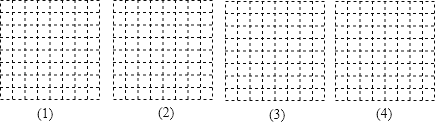
【题目】下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个边长为2![]() ,面积为6的等腰三角形.
,面积为6的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
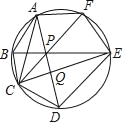
【题目】如图,圆内接六边形ABCDEF中AB=CD=EF,且三条对角线AD、BE、CF交于点P,CE与AD交于点Q,已知AC=26,CE=39,那么CQQE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
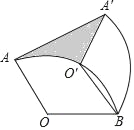
【题目】如图,将半径为6,圆心角为120°的扇形OAB绕点B顺时针旋转60°,点O,A的对应点分别为O′,A′,连接AA′,在图中阴影部分的面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com