
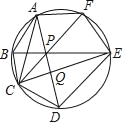
【题目】如图,圆内接六边形ABCDEF中AB=CD=EF,且三条对角线AD、BE、CF交于点P,CE与AD交于点Q,已知AC=26,CE=39,那么CQQE=_____.
【答案】324
【解析】
利用相似三角形的性质证明![]() =
=![]() =
=![]() =
=![]() =
=![]() ,设CQ=4k,QE=9k,构建方程求出k即可解决问题;
,设CQ=4k,QE=9k,构建方程求出k即可解决问题;
解:连AE,
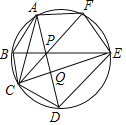
∵AB=CD=EF,
∴弧AB=弧CD=弧EF,
∴∠AEB=∠CED,
∴∠PED=∠BEC+∠CED=∠BEC+∠AEB=∠AEC,
又∵∠PDE=∠ACE,
∴△PDE∽△ACE,
∴![]() =
=![]() ,
,
∵弧CD=弧EF,
∴DE∥CF,
∴![]() =
=![]() ,∠CPD=∠PDE,
,∠CPD=∠PDE,
∵∠PED对BD弧,∠ADC对AC弧,
而DC弧=AB弧,
∴∠PED=∠ADC,
∴△PDC∽△DEP,
∴![]() =
=![]() ,即PC=
,即PC=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
由(1)的结论 ![]() =
=![]() 得,
得,![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
设CQ=4k,EQ=9k,
则有13k=39,
∴k=3,
∴CQ=12,EQ=27,
∴CQQE=324,
故答案为324.


科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
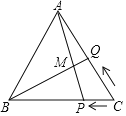
【题目】如图,等边△ABC的边长为8cm,点P从点C出发,以1cm/秒的速度由C向B匀速运动,点Q从点C出发,以2cm/秒的速度由C向A匀速运动,AP、BQ交于点M,当点Q到达A点时,P、Q两点停止运动,设P、Q两点运动的时间为t秒,若∠AMQ=60°时,则t的值是( )
A.1B.2C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十一黄金周期间,海洋中学决定组织部分优秀老师去北京旅游,天马旅行社推出如下收费标准:

(1)学校规定,人均旅游费高于700元,但又想低于1000元,那么该校所派人数应在什么范围内;
(2)已知学校已付旅游费27000元,问该校安排了多少名老师去北京旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
查看答案和解析>>
科目:初中数学 来源: 题型:
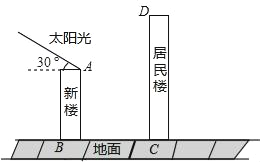
【题目】某住宅小区有一栋面朝正南的居民楼(如图),该居民楼的一楼高为6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.已知冬季正午的阳光与水平线的夹角为30°时.
(1)新楼的建造对超市以上的居民住房冬季正午的采光是否有影响,为什么?
(2)若要使超市冬季正午的采光不受影响,新楼应建在相距居民楼至少多少米的地方,为什么?(结果保留整数,参考数据:sin30°≈0.5,cos30°≈0.87,tan30°≈0.58)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G.
(1)猜想BG与EG的数量关系.并说明理由;
(2)延长DE,BA交于点H,其他条件不变,
①如图2,若∠ADC=60°,求![]() 的值;
的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出![]() 的值.(用含α的三角函数表示)
的值.(用含α的三角函数表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com