练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

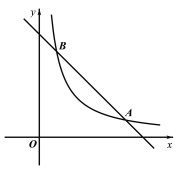
    【题目】如图，在平面直角坐标系xOy中，直线与函数的图象的两个交点分别为A（a，1）、B.

    （1）求，a的值及点B的坐标；

    （2）过点P（n，0）作x轴的垂线，与直线和函数的图象分别交于点M，N，当点M在点N上方时，写出n的取值范围.

    【答案】（1）点B的坐标为（1，5）；（2）.

    【解析】

    （1）将A点坐标（a，1）代入函数中即可求出m的值，然后将A的坐标代入一次函数解析式中即可求出k的值．
    （2）当点M在点N上方时，由题意可知PN<PM，此时y1>y2，这部分的图像中，一次函数的图像在反比例函数的图像的上方，即点A、B之间部分（不包括点A、B），根据图象可求出n的范围．

    （1）把A（a，1）代入函数中，

    ∴.

    ∴.

    把A（5，1）代入函数中，

    ∴.

    ∴.

    ∴

    解得，.

    ∴点B的坐标为（1，5）.

    （2）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

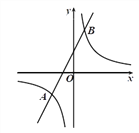
    【题目】如图，在平面直角坐标系中，一次函数与反比例函数交于点， ．

    （1）分别求出反比例函数和一次函数的表达式；

    （2）根据函数图象，直接写出不等式的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

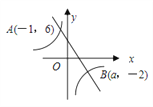
    【题目】（8分）如图，一次函数y1＝kx＋b（k≠0）和反比例函数y2＝（m≠0）的图像交于点A（－1，6）、B（a，－2）．

    （1）求一次函数与反比例函数的解析式；

    （2）根据图像直接写出y1＞y2时，x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，C是弧的中点，⊙O的切线BD交AC的延长线于点D,E是OB的中点，CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.

    ⑴求证：AC=CD.

    ⑵若OB=2,求BH的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的1．5倍．如果由甲、乙队先合做15天，那么余下的工程由甲队单独完成还需5天．

    （1）这项工程的规定时间是多少天？

    （2）已知甲队每天的施工费用为6500元，乙队每天的施工费用为3500元．为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙队合做来完成．则该工程施工费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

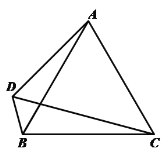
    【题目】如图，在等边△中，作，边CD、BD交于点D，连接AD.

    （1）请直接写出的度数；

    （2）求的度数；

    （3）用等式表示线段AC、BD、CD三者之间的数量关系，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：平行四边形ABCD中，对角线AC、BD相交于点O，BD=2AD，E，F，G分别是OC，OD，AB的中点．求证：

    （1）BE⊥AC；

    （2）EG=EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】边长为a，b的矩形发生形变后成为边长为a，b的平行四边形，如图1，ABCD中，，AB边上的高为h，我们把h与a的比值叫做这个平行四边形的“形变比”．

    画出图2中菱形ABCD形变前的图形．

    若图2中菱形ABCD的“形变比”为，求菱形ABCD形变前后的面积之比．

    当边长为3，4的矩形形变后成为一个内角是的平行四边形时，求这个平行四边形的“形变比”．

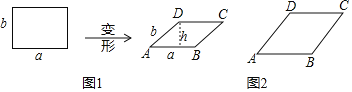
    查看答案和解析>>

    科目：初中数学 来源： 题型：

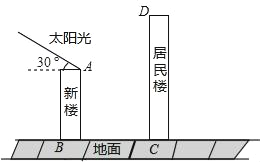
    【题目】某住宅小区有一栋面朝正南的居民楼（如图），该居民楼的一楼高为6米的小区超市，超市以上是居民住房．在该楼的前面15米处要盖一栋高20米的新楼．已知冬季正午的阳光与水平线的夹角为30°时．

    （1）新楼的建造对超市以上的居民住房冬季正午的采光是否有影响，为什么？

    （2）若要使超市冬季正午的采光不受影响，新楼应建在相距居民楼至少多少米的地方，为什么？（结果保留整数，参考数据：sin30°≈0.5，cos30°≈0.87，tan30°≈0.58）

    查看答案和解析>>

    同步练习册答案