
【题目】边长为a,b的矩形发生形变后成为边长为a,b的平行四边形,如图1,ABCD中,![]() ,AB边上的高为h,我们把h与a的比值叫做这个平行四边形的“形变比”.
,AB边上的高为h,我们把h与a的比值叫做这个平行四边形的“形变比”.
![]() 画出图2中菱形ABCD形变前的图形.
画出图2中菱形ABCD形变前的图形.
![]() 若图2中菱形ABCD的“形变比”为
若图2中菱形ABCD的“形变比”为![]() ,求菱形ABCD形变前后的面积之比.
,求菱形ABCD形变前后的面积之比.
![]() 当边长为3,4的矩形形变后成为一个内角是
当边长为3,4的矩形形变后成为一个内角是![]() 的平行四边形时,求这个平行四边形的“形变比”.
的平行四边形时,求这个平行四边形的“形变比”.
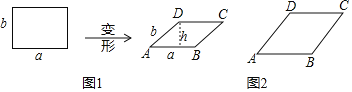
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园的绿化工程,甲、乙两队单独完成这项工程所需的时间比是5:3,两队共同施工15天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队共同施工15天完成任务后,学校付给他们20000元报酬,若按各自完成的工程量分配这笔钱,问甲、乙两队各应得到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
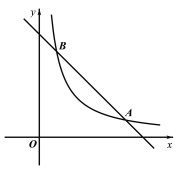
【题目】如图,在平面直角坐标系xOy中,直线![]() 与函数
与函数![]() 的图象的两个交点分别为A(a,1)、B.
的图象的两个交点分别为A(a,1)、B.
(1)求![]() ,a的值及点B的坐标;
,a的值及点B的坐标;
(2)过点P(n,0)作x轴的垂线,与直线![]() 和函数
和函数![]() 的图象分别交于点M,N,当点M在点N上方时,写出n的取值范围.
的图象分别交于点M,N,当点M在点N上方时,写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已知点![]() 的坐标(-1,4),点
的坐标(-1,4),点![]() 的位置如图所示
的位置如图所示
(1)写出图中点![]() 的坐标: ________;
的坐标: ________;
(2)求![]() 的面积;
的面积;
(3)画出![]() 关于
关于![]() 轴的对称图形,点
轴的对称图形,点![]() 的对称点分别为
的对称点分别为![]() ,写出
,写出![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校允许学生在同个系列的校服里选择不同款式,新生入学后,学校就新生对校服款式选择情况作了抽样调查,调查分为款式A、B、C、D四种,每位新生只能选择一种款式,现将调查统计结果制成了如下两幅不完整的统计图,请结合这两幅统计图,回答下列问题:
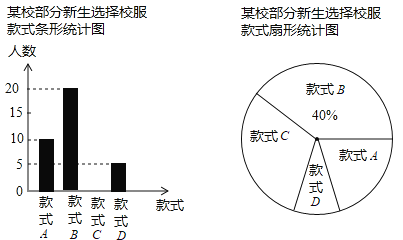
(1)在本次调查中,一共抽取了多少名新生,并补全条形统计图;
(2)若该校有847名新生,服装厂已生产了270套B款式的校服,请你按相关统计知识判断是否还要继续生产B款式的校服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠,使点D与点B重合,点C落在点C′的位置上.
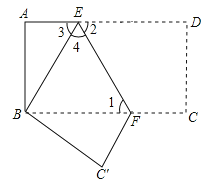
⑴若∠1=50°,求∠2、∠3的度数;
⑵若AB=7,DE=8,求CF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人同时同地沿同一路线开始攀登一座600米高的山,甲的攀登速度是乙的1.2倍,他比乙早20分钟到达顶峰.甲乙两人的攀登速度各是多少?如果山高为![]() 米,甲的攀登速度是乙的
米,甲的攀登速度是乙的![]() 倍,并比乙早
倍,并比乙早![]() 分钟到达顶峰,则两人的攀登速度各是多少?
分钟到达顶峰,则两人的攀登速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有
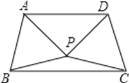
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com