
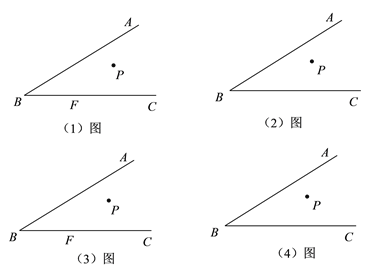
【题目】动手操作:请按要求作图.(规范作图,保留作图痕迹即可,不要求尺规作图)
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,
内一定点, ![]() 为射线
为射线![]() 边上一定点,请在射线
边上一定点,请在射线![]() 上找一点
上找一点![]() ,使得
,使得![]() 最小.
最小.
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,点
内一定点,点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 边上两个动点,请作出使得
边上两个动点,请作出使得![]() 最小的
最小的![]() 点和
点和![]() 点.
点.
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,点
内一定点,点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 边上两个动点,请作出使得
边上两个动点,请作出使得![]() 最小的
最小的![]() 点和
点和![]() 点.
点.
拓展应用:
(![]() )如图(
)如图(![]() ),
),![]() 为锐角三角形,
为锐角三角形, ![]() ,
, ![]() ,
, ![]() 的面积为
的面积为![]() ,点
,点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 三边
三边![]() 、
、![]() 、
、![]() 上的三个动点,请在图中作出满足条件的周长最小的
上的三个动点,请在图中作出满足条件的周长最小的![]() ,并求出
,并求出![]() 周长的最小值.
周长的最小值.
【答案】(1)作图见解析;(2)作图见解析;(3)作图见解析;(4)作图见解析, ![]() 的周长有最小值为11.
的周长有最小值为11.
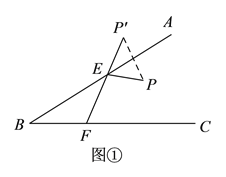
【解析】试题分析:(1)作点P关于直线AB的对称点P^',连接P^' F交AB于E,则此时PE+EF最小;
(2)作点P关于直线AB的对称点M,连接MP交AB于点N,过点M作MF⊥BC于F交AB于E,则此时PE+EF最小;
(3)作点P关于直线AB的对称点M,关于直线BC的对称点N,连接MN交AB于E,交BC于F,则此时PE+EF+PE最小;
(4)作点P关于线段AB的对称点M,关于直线BC的对称点N,连接MN交AB于E,交BC于点F,则此时△PEF的周长为MN的长度.
试题解析:解:(1)如图①,作点P关于直线AB的对称点P^',连接P^' F交AB于E,则此时PE+EF最小;
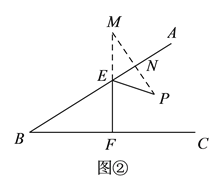
(![]() )如图②,作点P关于直线AB的对称点M,连接MP交AB于点N,过点M作MF⊥BC于F交AB于E,则此时PE+EF最小;
)如图②,作点P关于直线AB的对称点M,连接MP交AB于点N,过点M作MF⊥BC于F交AB于E,则此时PE+EF最小;
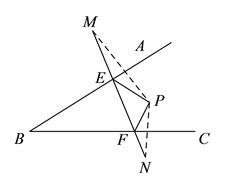
(3)如图③,作点P关于直线AB的对称点M,关于直线BC的对称点N,连接MN交AB于E,交BC于F,则此时PE+EF+PE最小;
(4)如图④,作点P关于线段AB的对称点M,关于直线BC的对称点N,连接MN交AB于E,交BC于点F,则此时△PEF的周长为MN的长度.
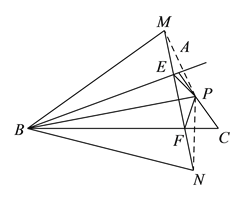
∵∠ABC=30°,∴∠MBN=60°且BM=BP=BN,∴△MBN为等边三角形,∴当BP⊥AC时,MN有最小值,即△PEF的周长有最小值, ![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断△ABC为直角三角形的是( )
A. a+b=c B. a:b:c=3:4:5 C. a=b=2c D. ∠A=∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
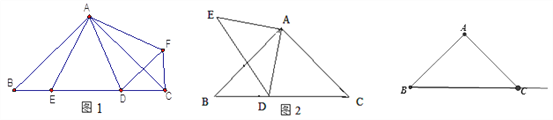
【题目】(1)如图1,在Rt△ABC 中, ![]() ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△![]() 绕点
绕点![]() 逆时针旋转90后,得到△
逆时针旋转90后,得到△![]() ,连接
,连接![]() .
.
(1)试说明:△![]() ≌△
≌△![]() ;
;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位在五月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位带队管理员工的费用,其余员工八折优惠.
【1】如果设参加旅游的员工共有a(a![]() )人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)
)人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)
【2】假如这个单位现组织包括管理员工在内的共20名员工到北京旅游,该单位选择哪一家旅行社比较优惠?请说明理由.
【3】如果计划在五月份外出旅游连续七天,设最中间一天的日期为![]() ,则这七天的日期之和为 .(用含
,则这七天的日期之和为 .(用含![]() 的代数式表示,并化简.)
的代数式表示,并化简.)
【4】假如这七天的日期之和为63的倍数,则他们可能于五月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADC都是等边三角形,点E,F同时分别从点B,A出发,以相同的速度各自沿BA,AD的方向运动到点A,D停止,连结EC,FC.

(1)在点E,F运动的过程中,∠ECF的大小是否随之变化?请说明理由.
(2)在点E,F运动的过程中,以A,E,C,F为顶点的四边形的面积变化了吗?请说明理由.
(3)连结EF,在图中找出所有和∠ACE相等的角,并说明理由.
(4)若点E,F在射线BA,射线AD上继续运动下去,(1)中的结论还成立吗?直接写出结论,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com