
【题目】如图,△ABC和△ADC都是等边三角形,点E,F同时分别从点B,A出发,以相同的速度各自沿BA,AD的方向运动到点A,D停止,连结EC,FC.

(1)在点E,F运动的过程中,∠ECF的大小是否随之变化?请说明理由.
(2)在点E,F运动的过程中,以A,E,C,F为顶点的四边形的面积变化了吗?请说明理由.
(3)连结EF,在图中找出所有和∠ACE相等的角,并说明理由.
(4)若点E,F在射线BA,射线AD上继续运动下去,(1)中的结论还成立吗?直接写出结论,不必说明理由.
【答案】(1)没有变化(2)没有变化(3)∠AFE=∠DCF=∠ACE(4)(1)中的结论仍成立
【解析】试题分析:(1)由于BE=AF,BC=AC,且∠B=∠CAF=60°,根据SAS可证得△BCE≌△ACF,即可得∠BCE=∠ACF,因此∠ECF=∠ACF+∠ACE=∠BCE+∠ACE=60°,因此∠ECF的度数是定值,不会改变.(2)由(1)的全等三角形知:△ACF、△BCE的面积相等,因此四边形AECF的面积可转化为△ABC的面积,因此当E、F分别在线段AB、AD上运动时,四边形AECF的面积不变.(3)同(1)可证得△ACE≌△DCF,得∠ACE=∠FCD;连接EF,由(1)(3)的全等三角形,易知CE=CF,且∠ECF=60°,因此△ECF是等边三角形,那么∠EFC=60°,然后根据平角的定义以及三角形内角和定理,证得∠AFE=∠FCD,进而可求得∠ACE相等的角是:∠ACE=∠AFE=∠FCD.(4)由于当E、F分别在BA、AD延长线上时,(1)的全等三角形依然成立,因此(1)的结论是成立的.
试题解析:
(1)没有变化.理由如下:
∵点E,F的速度相同,且同时运动,
∴BE=AF.
∵△ABC和△ADC都是等边三角形,
∴BC=AC,∠B=∠ACB=∠CAF=60°.
在△BCE和△ACF中,∵ 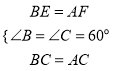
∴△BCE≌△ACF(SAS).∴∠BCE=∠ACF.
∴∠ECF=∠ACF+∠ACE=∠BCE+∠ACE=∠ACB=60°.
(2)没有变化.理由如下:
由(1)知,△BCE与△ACF的面积相等,
∴S四边形AECF=S△ACF+S△ACE=S△BCE+S△ACE=S△ABC.
∴四边形AECF的面积没有变化.
(3)∠AFE=∠DCF=∠ACE.理由如下:
∵△ABC和△ADC都是等边三角形,
∴∠EAC=∠FDC=60°,AB=AC=DC=AD.
∵BE=AF,∴AB-BE=AD-AF,即AE=DF.
∴△ACE≌△DCF(SAS).
∴∠ACE=∠DCF,EC=FC.
又∵∠ECF=60°,
∴△ECF是等边三角形,∴∠EFC=60°.
∴∠AFE+∠DFC=120°.
∵∠D=60°,∴∠DCF+∠DFC=120°.
∴∠AFE=∠DCF=∠ACE.
(4)(1)中的结论仍成立.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
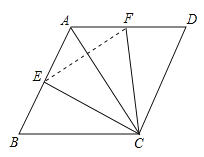
【题目】动手操作:请按要求作图.(规范作图,保留作图痕迹即可,不要求尺规作图)
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,
内一定点, ![]() 为射线
为射线![]() 边上一定点,请在射线
边上一定点,请在射线![]() 上找一点
上找一点![]() ,使得
,使得![]() 最小.
最小.
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,点
内一定点,点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 边上两个动点,请作出使得
边上两个动点,请作出使得![]() 最小的
最小的![]() 点和
点和![]() 点.
点.
(![]() )如图(
)如图(![]() ),
),![]() 是
是![]() 内一定点,点
内一定点,点![]() 、
、![]() 分别为射线
分别为射线![]() 、
、![]() 边上两个动点,请作出使得
边上两个动点,请作出使得![]() 最小的
最小的![]() 点和
点和![]() 点.
点.
拓展应用:
(![]() )如图(
)如图(![]() ),
),![]() 为锐角三角形,
为锐角三角形, ![]() ,
, ![]() ,
, ![]() 的面积为
的面积为![]() ,点
,点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 三边
三边![]() 、
、![]() 、
、![]() 上的三个动点,请在图中作出满足条件的周长最小的
上的三个动点,请在图中作出满足条件的周长最小的![]() ,并求出
,并求出![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
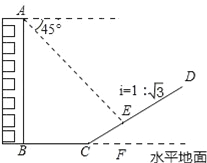
【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道,若点A、B在数轴上分别表示有理数a、b,A、B两点间的距离表示为AB.则AB=|a-b|.所以式子|x-3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.根据上述材料,解答下列问题:
![]()
(1)数轴上表示2和5两点之间的距离是___________;数轴上表示1和-3的两点之间的距离是__________
(2)数轴上表示x和2两点之间的距离表示为___________
(3)若,则 ![]() =5,则x=__________;
=5,则x=__________;
(4)式子|x-3|+|x+1|=8 ,则x的值为_____________;
(5) 若x表示一个有理数,式子|x-3|+|x+1|的最小值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(要求写出计算过程)
(1)5﹣(﹣6)×2÷22
(2)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣63)
)×(﹣63)
(3)(﹣2)3×( ![]() )2﹣|﹣1﹣2|
)2﹣|﹣1﹣2|
(4)![]() +
+ ![]() ﹣(﹣
﹣(﹣ ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y=-kx(k<0) 下列说法错误的是( )
A.它是正比例函数B.图象经过点(1,-k)
C.图象经过第一、三象限D.当x>0时,y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
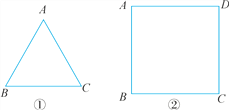
【题目】(1)如图①,△ABC是等边三角形,△ABC所在平面上有一点P,使△PAB,△PBC,△PAC都是等腰三角形,问:具有这样性质的点P有几个?在图中画出来.
(2)如图②,正方形ABCD所在的平面上有一点P,使△PAB,△PBC,△PCD,△PDA都是等腰三角形,问:具有这样性质的点P有几个?在图中画出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人去水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.B家的规定如下表:
数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
[表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100﹣1500)]
(1)如果他批发600千克苹果,则他在A 家批发需要元,在B家批发需要元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要元,在B家批发需要元(用含x的代数式表示);
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图形1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为:1+2+3+…+n= ![]() .
.
(1)当n=15时,我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,….,则最底层最左边这个圆圈中的数是多少?当有n层时,最底层最左边这个圆圈中的数又是多少?(只列代数式不要求化简)
(2)当n=19时,我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣25,﹣24,﹣23,…则这时最底层最左边这个圆圈中的数是多少?并求出此时所有圆圈中各数的绝对值之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com