
【题目】如图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图形1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为:1+2+3+…+n= ![]() .
.
(1)当n=15时,我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数1,2,3,4,….,则最底层最左边这个圆圈中的数是多少?当有n层时,最底层最左边这个圆圈中的数又是多少?(只列代数式不要求化简)
(2)当n=19时,我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数﹣25,﹣24,﹣23,…则这时最底层最左边这个圆圈中的数是多少?并求出此时所有圆圈中各数的绝对值之和.
【答案】
(1)
解:当n=15时,图中共有:1+2+3+…+15=120个圆圈;
最底层最左边这个圆圈中的数是14×15× ![]() +1=106
+1=106
(2)
解:图4中所有圆圈中共有1+2+3+…+19= ![]() =190个数,其中25个负数,1个0,164个正数,
=190个数,其中25个负数,1个0,164个正数,
∴最底层最左边这个圆圈中的数是18×19× ![]() +1=172,
+1=172,
所以图4中所有圆圈中各数的绝对值之和=|﹣25|+|﹣24|+…+|﹣1|+0+1+2+…+164=(1+2+3+…+25)+(1+2+3+…+164)=325+13530=13855
【解析】(1)根据图形中圆圈的个数变化规律得出答案即可;(2)19层时最底层最左边这个圆圈中的数是第18层的最后一个数加1;首先计算圆圈的个数,从而分析出25个负数后,又有多少个正数.


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADC都是等边三角形,点E,F同时分别从点B,A出发,以相同的速度各自沿BA,AD的方向运动到点A,D停止,连结EC,FC.

(1)在点E,F运动的过程中,∠ECF的大小是否随之变化?请说明理由.
(2)在点E,F运动的过程中,以A,E,C,F为顶点的四边形的面积变化了吗?请说明理由.
(3)连结EF,在图中找出所有和∠ACE相等的角,并说明理由.
(4)若点E,F在射线BA,射线AD上继续运动下去,(1)中的结论还成立吗?直接写出结论,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
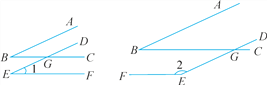
(1)∠1= ,∠2= .
(2)请观察∠1,∠2与∠ABC分别有怎样的关系,请你由此归纳一个真命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B=∠DEC,AB=DE,要推得△ABC≌△DEC;
(1)若以“SAS”为依据,还缺条件______________;
(2)若以“ASA”为依据,还缺条件__________________;
(3)若以“AAS”为依据,还缺条件_____________________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的A,B,C,D四点所表示的数分别为a、b、c、d,且O为原点.根据图中各点位置,判断|a﹣c|之值与下列何者不同?( ) ![]()
A.|a|+|b|+|c|
B.|a﹣b|+|c﹣b|
C.|a﹣d|﹣|d﹣c|
D.|a|+|d|﹣|c﹣d|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com