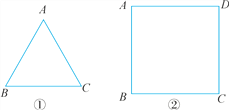
【题目】(1)如图①，△ABC是等边三角形，△ABC所在平面上有一点P，使△PAB，△PBC，△PAC都是等腰三角形，问：具有这样性质的点P有几个？在图中画出来．

(2)如图②，正方形ABCD所在的平面上有一点P，使△PAB，△PBC，△PCD，△PDA都是等腰三角形，问：具有这样性质的点P有几个？在图中画出来．

参考答案：

【答案】（1）10个（2）9个

【解析】试题分析:（1）点P在三角形的内部时,点P到△ABC的三个顶点的距离相等,点P是三角形三边垂直平分线的交点,所以点P是三角形的外心;点P在三角形外部时,每条边的垂直平分线上的点只要能够使顶点这条边的两端点连接而成的三角形是等腰三角形即可.

（2）根据正方形的性质可得,满足这样的点首先有:两条对角线的交点,再以四个顶点为圆心,以正方形的边长为半径画圆,在正方形里面和外面的交点一共有8个.

试题解析:具体作法如下,

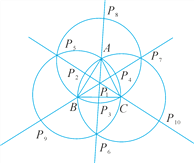
（1）10个,如解图①,当点P在△ABC内部时,P是边AB,BC,CA的垂直平分线的交点;当点P在△ABC外部时,P是以三角形各顶点为圆心,边长为半径的圆与三条垂直平分线的交点,每条垂直平分线上得3个交点.故具有这样性质的点P共有10个.

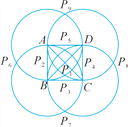
(2)9个,如解图②,两条对角线的交点是1个,以正方形各顶点为圆心,边长为半径画圆,在正方形里面和外面的交点一共有8个,故具有这样性质的点P共有9个.

点睛:本题主要考查垂直平分线的性质,正方形性质,等腰三角形的性质,要求学生熟练掌握利用垂直平分线的性质,正方形和等腰三角形的性质找出符合条件的点.

关闭